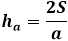Wysokość Trójkąta

W dowolnym trójkącie (gdzie wszystkie boki mają różne długości), wysokości poprowadzone do boków , środkowe i dwusieczne reprezentują zupełnie różne linie. Aby znaleźć wysokość w trójkącie, nie można używać właściwości środkowej lub dwusiecznej jak w trójkątach równoramiennych lub równobocznych, więc trzeba zastosować inne metody.

Jedna z podobnych metod polega na użyciu wspólnego parametru trójkąta - pola. Algorytm obliczeń opiera się na fakcie, że pole trójkąta nieprostokątnego można znaleźć na kilka sposobów, w tym poprzez wysokość. Znając trzy boki trójkąta, można znaleźć jego pole używając wzoru Herona, a następnie używając innego wzoru na pole, wyrazić przez nie wysokość.

Aby obliczyć pole trójkąta za pomocą wzoru Herona, najpierw trzeba obliczyć półobwód trójkąta. Jak sama nazwa wskazuje, półobwód to obwód, czyli suma długości wszystkich trzech boków, podzielona przez dwa.

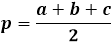
Sam wzór na pole to iloczyn półobwodu z jego różnicą od każdego boku, całość pod pierwiastkiem kwadratowym.

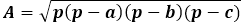
Z drugiej strony, to samo pole trójkąta poprzez wysokość równa się połowie iloczynu boku trójkąta z wysokością opuszczoną na niego. W ten sposób wysokość równa się dwukrotności pola podzielonego przez bok trójkąta. Z poprzedniego wzoru można wyrazić pole poprzez trzy boki trójkąta i zastąpić je we wzorze na wysokość.

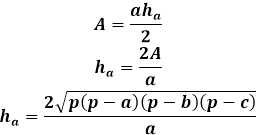
Ten wzór na wysokość poprzez boki trójkąta ma zastosowanie do dowolnych trójkątów, nieprostokątnych, równoramiennych lub równobocznych, w przypadku braku innych.

Obliczanie wysokości trójkąta znając trzy boki wymaga długiej drogi poprzez wzory na pole. Wysokość trójkąta wyrażona przez pole jest związana tylko z bokiem, na który jest opuszczona, więc niezwykle ważne jest, aby prawidłowo wskazać kolejność boków dla kalkulatora i w obliczeniach ręcznych, aby zastąpić odpowiedni bok we wzorze na wysokość.

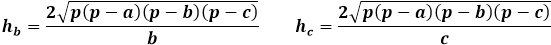
Wzór na wysokość dowolnego trójkąta poprzez pole