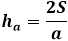Altura do Triângulo

Em um triângulo qualquer (onde todos os lados têm comprimentos diferentes), alturas traçadas para os lados , medianas e bissetrizes representam linhas completamente diferentes. Para encontrar a altura em um triângulo, não se pode usar as propriedades da mediana ou da bissetriz como nos triângulos isósceles ou equiláteros, então outros métodos devem ser usados.

Um dos métodos semelhantes envolve o uso de um parâmetro comum do triângulo - a área. O algoritmo de cálculo é baseado no fato de que a área de um triângulo escaleno pode ser encontrada de várias maneiras, incluindo através da altura. Conhecendo os três lados do triângulo, você pode encontrar sua área usando a fórmula de Heron, e então, usando outra fórmula de área, expressar a altura através dela.

Para calcular a área de um triângulo usando a fórmula de Heron, primeiro você precisa calcular o semiperímetro do triângulo. Como o nome sugere, o semiperímetro é o perímetro, ou a soma dos comprimentos de todos os três lados, dividido por dois.

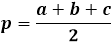
A fórmula da área em si é o produto do semiperímetro com sua diferença de cada lado, toda a expressão estando sob a raiz quadrada.

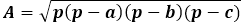
Por outro lado, a mesma área do triângulo através da altura é igual a metade do produto do lado do triângulo com a altura traçada sobre ele. Assim, a altura é igual ao dobro da área dividida pelo lado do triângulo. Da fórmula anterior, você pode expressar a área através dos três lados do triângulo e substituí-la na fórmula da altura.

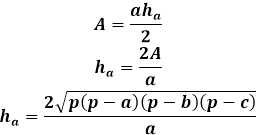
Esta fórmula de altura através dos lados do triângulo é aplicável a qualquer triângulo, escaleno, isósceles ou equilátero, na ausência de outros.

Calcular a altura de um triângulo conhecendo os três lados requer um longo caminho usando fórmulas de área. A altura do triângulo expressa através da área está relacionada apenas ao lado sobre o qual é traçada, por isso é extremamente importante indicar adequadamente a ordem dos lados para a calculadora e no cálculo manual substituir o lado apropriado na fórmula da altura.

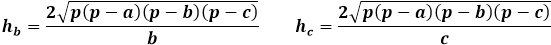
Fórmula da altura de um triângulo qualquer através da área