Transpunerea matricelor

O matrice transpusă este obținută prin înlocuirea rândurilor matricii originale cu coloane sau a coloanelor sale cu rânduri.

Proprietățile transpunerii matricelor:
O matrice transpusă de două ori este egală cu matricea originalăA^TT(A^T)^T=A
Matricea transpusă a unei sume este egală cu suma matricelor transpuse(A + B)^T=A^T+B^T
Matricea transpusă a unui produs este egală cu produsul matricelor transpuse ale factorilor, luate în ordine inversă(A × B)^T=A^T×B^T

Pentru a obține o matrice transpusă, trebuie să efectuați una dintre următoarele acțiuni cu matricea originală:

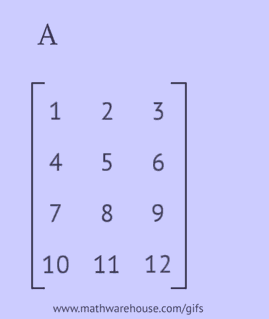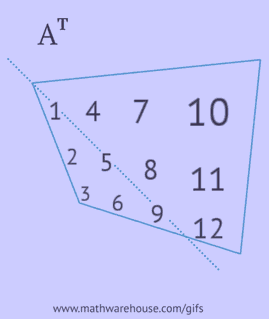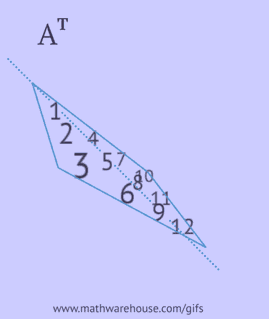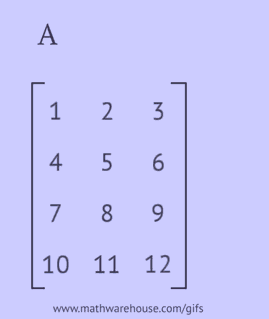
- scrieți fiecare dintre rândurile sale ca o coloană în aceeași ordine;
- scrieți fiecare dintre coloanele sale ca un rând în aceeași ordine;
- reflectați elementele sale față de diagonala principală, începând din colțul din stânga sus și continuând spre dreapta și în jos până la marginea de jos sau dreapta.

Matricile transformate în transpusă sunt folosite pentru rezolvarea sistemelor de ecuații algebrice, găsirea matricei inverse, precum și în alte sarcini de algebră liniară.