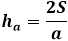Výška trojuholníka

V ľubovoľnom trojuholníku (kde všetky strany majú rôznu dĺžku), výšky nakreslené k stranám , stredné čiary a bisektory predstavujú úplne odlišné čiary. Na nájdenie výšky v trojuholníku nemôžete použiť vlastnosti strednej čiary alebo bisektory ako u rovnoramenných alebo rovnostranných trojuholníkov, preto sa musia použiť iné metódy.

Jedna z podobných metód zahŕňa použitie spoločného parametra trojuholníka - plochy. Výpočtový algoritmus je založený na tom, že plocha všeobecného trojuholníka sa dá nájsť niekoľkými spôsobmi, vrátane výšky. Poznanie troch strán trojuholníka, môžete nájsť jeho plochu pomocou Heronovho vzorca, a potom pomocou iného vzorca pre plochu, vyjadriť výšku cez ňu.

Na výpočet plochy trojuholníka pomocou Heronovho vzorca, najprv musíte vypočítať polovičný obvod trojuholníka. Ako názov napovedá, polovičný obvod je obvod, alebo súčet dĺžok všetkých troch strán, delený dvoma.

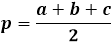
Samotný vzorec pre plochu je súčin polovičného obvodu s jeho rozdielom od každej strany, celý výraz je pod odmocninou.

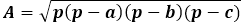
Na druhej strane, tá istá plocha trojuholníka cez výšku sa rovná polovici súčinu strany trojuholníka s výškou na ňu spustenou. Takže výška je rovná dvakrát plocha delená stranou trojuholníka. Z predchádzajúceho vzorca môžete vyjadriť plochu cez tri strany trojuholníka a nahradiť ju vo vzorci pre výšku.

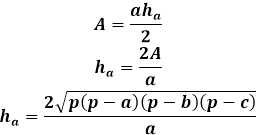
Tento vzorec pre výšku cez strany trojuholníka je použiteľný pre všetky trojuholníky, všeobecné, rovnoramenné alebo rovnostranné, v prípade neexistencie iných.

Výpočet výšky trojuholníka poznajúc tri strany vyžaduje dlhú cestu pomocou vzorcov pre plochu. Výška trojuholníka vyjadrená cez plochu sa vzťahuje iba k strane, na ktorú je spustená, takže je mimoriadne dôležité správne označiť poradie strán pre kalkulačku a v manuálnom výpočte nahradiť vhodnú stranu do vzorca pre výšku.

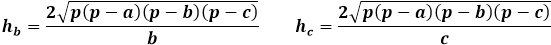
Vzorec pre výšku ľubovoľného trojuholníka cez plochu