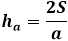Višina Trikotnika

V poljubnem trikotniku (kjer so vse stranice različnih dolžin), višine, narisane na stranice, mediane in bisektrise predstavljajo popolnoma različne črte. Za iskanje višine v trikotniku ne morete uporabiti lastnosti mediane ali bisektrise, kot pri enakokrakih ali enakostraničnih trikotnikih, zato je treba uporabiti druge metode.

Ena izmed podobnih metod vključuje uporabo skupnega parametra trikotnika - površine. Algoritem izračuna temelji na dejstvu, da je površino splošnega trikotnika mogoče izračunati na več načinov, vključno z višino. Z poznavanjem treh stranic trikotnika lahko najdete njegovo površino z uporabo Heronove formule, nato pa z uporabo druge formule za površino izrazite višino skozi njo.

Za izračun površine trikotnika z uporabo Heronove formule morate najprej izračunati polovični obseg trikotnika. Kot nakazuje ime, je polovični obseg obseg, oziroma vsota dolžin vseh treh stranic, deljena z dvema.

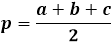
Sama formula za površino je produkt polovičnega obsega in njegove razlike od vsake stranice, celoten izraz pa je pod kvadratnim korenom.

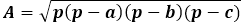
Po drugi strani pa je ista površina trikotnika skozi višino enaka polovici produkta trikotnikove stranice z višino spuščeno nanjo. Tako je višina enaka dvakratniku površine deljenemu s stranico trikotnika. Iz prejšnje formule lahko izrazite površino skozi tri stranice trikotnika in jo nadomestite v formuli za višino.

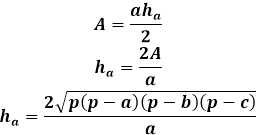
Ta formula za višino skozi stranice trikotnika je uporabna za katerikoli trikotnik, splošni, enakokraki ali enakostranični, v odsotnosti drugih.

Izračun višine trikotnika z znanjem treh stranic zahteva dolgo pot skozi formule za površino. Višina trikotnika, izražena skozi površino, je povezana le s stranico, na katero je spuščena, zato je zelo pomembno, da pravilno navedete vrstni red stranic za kalkulator in pri ročnem izračunu nadomestite ustrezno stranico v formulo za višino.

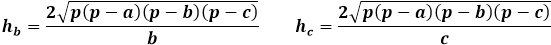
Formula za višino poljubnega trikotnika skozi površino