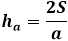Triangelns Höjd

I en godtycklig triangel (där alla sidor är av olika längd), höjder dragna till sidorna , medianer och bisektriser representerar helt olika linjer. För att hitta höjden i en triangel kan du inte använda egenskaperna hos medianen eller bisektrisen som för likbenta eller liksidiga trianglar, så andra metoder måste användas.

En av de liknande metoderna innebär att använda en gemensam parameter av triangeln - arean. Beräkningsalgoritmen är baserad på att arean av en godtycklig triangel kan hittas på flera sätt, inklusive genom höjden. Genom att känna till de tre sidorna av triangeln kan du hitta dess area med Herons formel, och sedan med en annan areaformel uttrycka höjden genom den.

För att beräkna arean av en triangel med Herons formel måste du först beräkna halvomkretsen av triangeln. Som namnet antyder är halvomkretsen omkretsen, eller summan av längderna på alla tre sidor, delat med två.

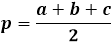
Själva areaformeln är produkten av halvomkretsen med dess skillnad från varje sida, hela uttrycket är under kvadratroten.

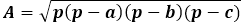
Å andra sidan, samma area av triangeln genom höjden är lika med halva produkten av triangelsidan med höjden dragen till den. Således är höjden lika med dubbla arean delad med triangelsidan. Från den föregående formeln kan du uttrycka arean genom de tre sidorna av triangeln och ersätta den i höjdformeln.

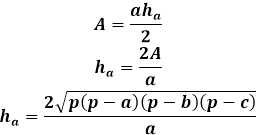
Denna höjdformel genom triangels sidor är tillämplig för alla trianglar, godtyckliga, likbenta eller liksidiga, i avsaknad av andra.

Att beräkna höjden av en triangel som känner till de tre sidorna kräver en lång väg med användning av areaformler. Höjden av triangeln uttryckt genom arean är endast relaterad till sidan den är dragen på, så det är extremt viktigt att korrekt ange ordningen på sidorna för kalkylatorn och vid manuell beräkning för att ersätta rätt sida i höjdformeln.

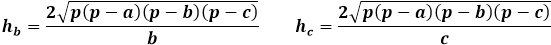
Höjdformel av en godtycklig triangel genom arean