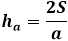ความสูงของสามเหลี่ยม

ในสามเหลี่ยมใดๆ (ที่ซึ่งด้านทั้งหมดมีความยาวต่างกัน), ความสูงที่ถูกวาดไปยังด้าน , เส้นแยก และ เส้นแบ่งกลาง เป็นเส้นที่แตกต่างกันโดยสิ้นเชิง การหาความสูงในสามเหลี่ยม คุณไม่สามารถใช้คุณสมบัติของเส้นแยกหรือเส้นแบ่งกลางได้เช่นในสามเหลี่ยมหน้าจั่วหรือสามเหลี่ยมด้านเท่า ดังนั้นต้องใช้วิธีการอื่น

หนึ่งในวิธีที่คล้ายกันเกี่ยวข้องกับการใช้พารามิเตอร์ร่วมของสามเหลี่ยม - พื้นที่ อัลกอริทึมการคำนวณอิงตามข้อเท็จจริงที่ว่าพื้นที่ของสามเหลี่ยมด้านไม่เท่ากันสามารถหาได้หลายวิธี รวมถึงผ่านทางความสูง ทราบความยาวด้านทั้งสามของสามเหลี่ยม คุณสามารถหาพื้นที่ของมันโดยใช้สูตรของเฮอรอน, และจากนั้นใช้สูตรพื้นที่อีกสูตรหนึ่ง แสดงความสูงผ่านทางนั้น

ในการคำนวณพื้นที่ของสามเหลี่ยมโดยใช้สูตรของเฮอรอน คุณต้องคำนวณเส้นรอบรูปครึ่งหนึ่งของสามเหลี่ยมก่อน ตามชื่อที่แนะนำ เส้นรอบรูปครึ่งหนึ่งคือเส้นรอบรูป หรือผลรวมของความยาวของด้านทั้งสาม หารด้วยสอง

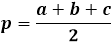
สูตรพื้นที่ตัวเองคือผลคูณของเส้นรอบรูปครึ่งหนึ่งกับความแตกต่างจากแต่ละด้าน การแสดงออกทั้งหมดอยู่ภายใต้รากที่สอง

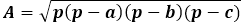
ในทางกลับกัน พื้นที่เดียวกันของสามเหลี่ยมผ่านทางความสูงเท่ากับครึ่งหนึ่งของผลคูณของด้านสามเหลี่ยมกับความสูงที่ลดลงไปถึงมัน ดังนั้นความสูงเท่ากับสองเท่าของพื้นที่หารด้วยด้านสามเหลี่ยม จากสูตรก่อนหน้านี้ คุณสามารถแสดงพื้นที่ผ่านทางด้านทั้งสามของสามเหลี่ยมและแทนที่ในสูตรความสูง

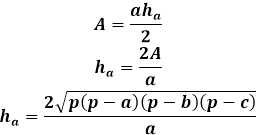
สูตรความสูงนี้ผ่านทางด้านสามเหลี่ยมสามารถใช้ได้กับสามเหลี่ยมใดๆ ไม่ว่าจะเป็นสามเหลี่ยมด้านไม่เท่ากัน สามเหลี่ยมหน้าจั่ว หรือสามเหลี่ยมด้านเท่า ในกรณีที่ไม่มีอย่างอื่น

การคำนวณความสูงของสามเหลี่ยมเมื่อทราบด้านทั้งสามต้องการเส้นทางยาวผ่านสูตรพื้นที่ ความสูงของสามเหลี่ยมแสดงผ่านทางพื้นที่เกี่ยวข้องเฉพาะกับด้านที่มันลดลง ดังนั้นจึงสำคัญมากที่จะระบุลำดับของด้านสำหรับเครื่องคำนวณและในการคำนวณด้วยตนเองเพื่อแทนที่ด้านที่เหมาะสมในสูตรความสูง

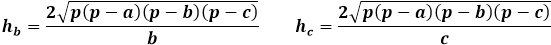
สูตรความสูงของสามเหลี่ยมใดๆ ผ่านทางพื้นที่