Додавання дробів
Додавання дробів з однаковими знаменниками:
Визначення: Сумою дробів з однаковими знаменниками називається дріб, чисельник якого дорівнює сумі чисельників вихідних дробів, а знаменник дорівнює знаменнику обох дробів.Формула
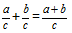
Додамо два дроби з однаковими знаменниками
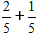
За формулою, додаємо чисельники, а знаменник залишаємо тим самим
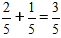
Важливо: Якщо можливо, у кінцевій відповіді записуємо спрощений дріб.
Приклад:
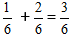 При скороченні дробу отримуємо число 1/2
При скороченні дробу отримуємо число 1/2 Додавання дробів з різними знаменниками:
Визначення: Щоб знайти суму дробів з різними знаменниками, спочатку приведіть дроби до спільного знаменника, а тоді додайте їх, як дроби з однаковими знаменниками.Задача:
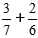
Процес рішення:
1) Приводимо дроби до спільного знаменника.
Для цього знаходимо НСК - найменше спільне кратне, для знаменників 7 і 6, це число є 42.
Ділимо число 42 на знаменники дробів 3/7 і 2/6
Таким чином, ми знайшли додаткові множники.
Далі множимо дроби на додаткові множники і отримуємо вираз:
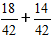
2) Додаємо дроби.
У нашому випадку дріб можна скоротити на 2, і в кінцевій відповіді ми записуємо число 16/21
Додавання дробу і цілого числа:
Визначення: Щоб додати дріб до цілого числа, спочатку представте ціле число як дріб із знаменником, рівним 1.Алгоритм обчислення:
1) Приводимо дроби до спільного знаменника.
2) Додаємо дроби
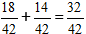
3) Якщо можливо, спрощуємо отриманий дріб.
4) Якщо результат є неправильним дробом, обчислюємо з нього цілу частину.
Приклад:
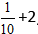
Рішення:
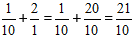
Обчислюємо цілу частину, і отримуємо відповідь
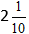
Додавання змішаних дробів:
Визначення: Щоб додати змішані дроби потрібно окремо додати цілі частини, і окремо додати дробові частини.Формула
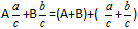
Приклад:
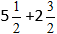
Підставляємо числа у формулу:
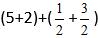
Отримуємо:
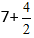
З дробу обчислюємо цілу частину, оскільки він неправильний, і отримуємо вираз 7+2=9.
