Транспонування матриці

Транспонована матриця отримується шляхом заміни рядків початкової матриці на стовпці або її стовпців на рядки.

Властивості транспонування матриці:
Матриця, транспонована двічі, дорівнює початковій матриці A^TT(A^T)^T=A
Транспонована матриця суми дорівнює сумі транспонованих матриць (A + B)^T=A^T+B^T
Транспонована матриця добутку дорівнює добутку транспонованих матриць множників, взятих в зворотньому порядку (A × B)^T=A^T×B^T

Щоб отримати транспоновану матрицю, потрібно виконати одну з наступних дій з початковою матрицею:

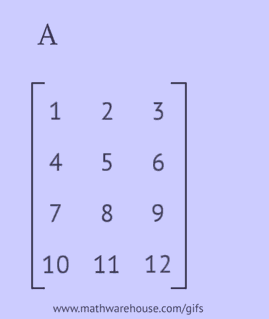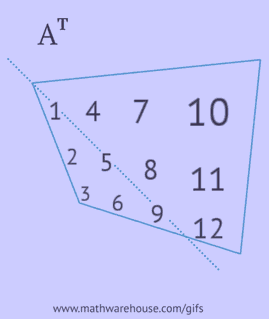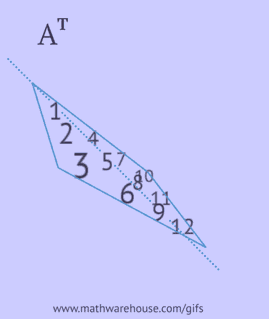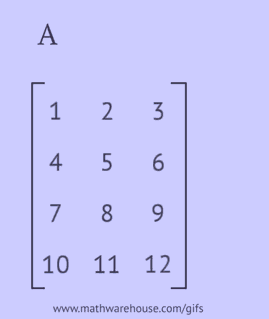
- записати кожен її рядок як стовпець у тому ж порядку;
- записати кожен її стовпець як рядок у тому ж порядку;
- відобразити її елементи відносно головної діагоналі, починаючи з верхнього лівого кута і продовжуючи вправо і вниз, поки не буде досягнутий нижній або правий край.

Матриці, перетворені в транспоновані, використовуються для розв'язання систем алгебраїчних рівнянь, знаходження оберненої матриці, а також в інших задачах лінійної алгебри.