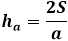Висота трикутника

У довільному трикутнику (де всі сторони мають різну довжину), висоти, проведені до сторін , медіани і бісектриси представляють собою абсолютно різні лінії. Щоб знайти висоту в трикутнику, не можна використовувати властивості медіани або бісектриси, як у рівнобедрених або рівносторонніх трикутниках, тому потрібно використовувати інші методи.

Один з подібних методів полягає у використанні загального параметра трикутника - площі. Алгоритм обчислення базується на тому, що площу довільного трикутника можна знайти кількома способами, включаючи через висоту. Знаючи три сторони трикутника, ви можете знайти його площу за формулою Герона, а потім, використовуючи іншу формулу площі, виразити через неї висоту.

Щоб обчислити площу трикутника за формулою Герона, спочатку потрібно обчислити напівпериметр трикутника. Як випливає з назви, напівпериметр дорівнює периметру, або сумі довжин всіх трьох сторін, поділеній на два.

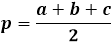
Сама формула площі є добутком напівпериметра на різницю з кожною стороною, весь вираз перебуває під квадратним коренем.

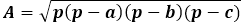
З іншого боку, та ж площа трикутника через висоту дорівнює половині добутку сторони трикутника на висоту, опущену на неї. Таким чином, висота дорівнює подвоєній площі, поділеній на сторону трикутника. З попередньої формули можна виразити площу через три сторони трикутника і підставити її у формулу висоти.

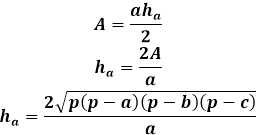
Ця формула висоти через сторони трикутника застосовна для будь-яких трикутників, довільних, рівнобедрених або рівносторонніх, за відсутності інших.

Обчислення висоти трикутника, знаючи три сторони, вимагає довгого шляху через формули площі. Висота трикутника, виражена через площу, пов'язана лише зі стороною, на яку вона опущена, тому надзвичайно важливо правильно вказати порядок сторін для калькулятора і при ручному обчисленні підставити відповідну сторону у формулу висоти.

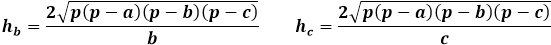
Формула висоти довільного трикутника через площу