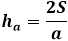Chiều cao tam giác

Trong một tam giác bất kỳ (nơi tất cả các cạnh có độ dài khác nhau), chiều cao được vẽ đến các cạnh, trung tuyến và đường phân giác đại diện cho các đường hoàn toàn khác nhau. Để tìm chiều cao trong một tam giác, bạn không thể sử dụng các thuộc tính của trung tuyến hoặc đường phân giác như đối với tam giác cân hoặc đều, vì vậy các phương pháp khác phải được sử dụng.

Một trong những phương pháp tương tự liên quan đến việc sử dụng một tham số chung của tam giác - diện tích. Thuật toán tính toán dựa trên thực tế rằng diện tích của một tam giác không đều có thể được tìm thấy theo nhiều cách, bao gồm cả qua chiều cao. Biết ba cạnh của tam giác, bạn có thể tìm diện tích của nó bằng công thức Heron, sau đó sử dụng công thức diện tích khác, biểu thị chiều cao thông qua nó.

Để tính diện tích của tam giác bằng công thức Heron, trước tiên bạn cần tính nửa chu vi của tam giác. Như tên gọi, nửa chu vi là chu vi, hoặc tổng độ dài của cả ba cạnh, chia cho hai.

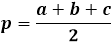
Công thức diện tích chính là tích của nửa chu vi với sự khác biệt của nó với từng cạnh, toàn bộ biểu thức nằm dưới căn bậc hai.

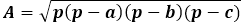
Mặt khác, cùng diện tích của tam giác qua chiều cao bằng một nửa tích của cạnh tam giác với chiều cao hạ xuống nó. Do đó, chiều cao bằng hai lần diện tích chia cho cạnh tam giác. Từ công thức trước đó, bạn có thể biểu thị diện tích thông qua ba cạnh của tam giác và thay thế nó vào công thức chiều cao.

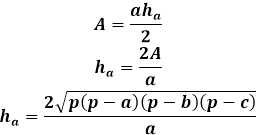
Công thức chiều cao này thông qua các cạnh của tam giác áp dụng cho mọi tam giác, không đều, cân, hoặc đều, khi không có các phương pháp khác.

Tính toán chiều cao của tam giác biết ba cạnh đòi hỏi một quá trình dài sử dụng công thức diện tích. Chiều cao của tam giác được biểu thị qua diện tích chỉ liên quan đến cạnh nó được hạ xuống, vì vậy cực kỳ quan trọng là phải chỉ định đúng thứ tự của các cạnh cho máy tính và trong tính toán thủ công để thay thế cạnh thích hợp vào công thức chiều cao.

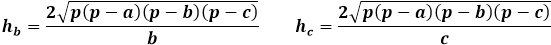
Công thức chiều cao của một tam giác bất kỳ thông qua diện tích