Matrixtransposition

Eine transponierte Matrix wird erhalten, indem die Zeilen der ursprünglichen Matrix gegen Spalten oder ihre Spalten gegen Zeilen ausgetauscht werden.

Eigenschaften der Matrixtransposition:
Eine zweimal transponierte Matrix ist gleich der ursprünglichen Matrix A^TT(A^T)^T=A
Die transponierte Matrix einer Summe ist gleich der Summe der transponierten Matrizen (A + B)^T=A^T+B^T
Die transponierte Matrix eines Produkts ist gleich dem Produkt der transponierten Matrizen der Faktoren, in umgekehrter Reihenfolge genommen (A × B)^T=A^T×B^T

Um eine transponierte Matrix zu erhalten, müssen Sie eine der folgenden Aktionen mit der ursprünglichen Matrix durchführen:

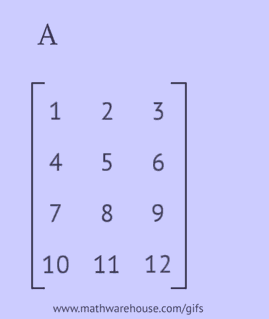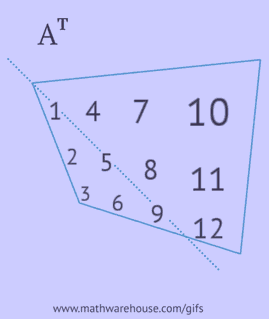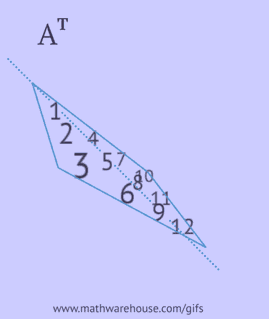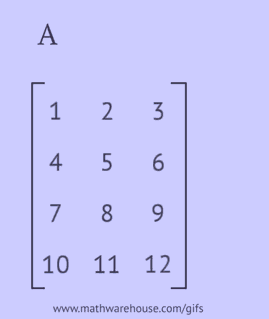
- schreiben Sie jede ihrer Zeilen in derselben Reihenfolge als Spalte;
- schreiben Sie jede ihrer Spalten in derselben Reihenfolge als Zeile;
- spiegeln Sie ihre Elemente relativ zur Hauptdiagonale, beginnend in der oberen linken Ecke und fortschreitend nach rechts und unten, bis der untere oder rechte Rand erreicht ist.

Matrizen, die in transponierte umgewandelt wurden, werden zur Lösung von Systemen algebraischer Gleichungen, zum Finden der inversen Matrix sowie in anderen Aufgaben der linearen Algebra verwendet.