Diagonales del Trapecio
Un trapecio es un cuadrilátero no convencional en el que dos de los lados – las bases del trapecio, son paralelas entre sí. Si trazas diagonales en un trapecio, forman una serie de triángulos semejantes, y las relaciones proporcionales de sus lados conducen a la propiedad principal del trapecio, combinando las diagonales del trapecio y sus cuatro lados:
d12+d22=c2+d2+2ab , donde a y b – estas son las bases del trapecio, y c y d – sus lados laterales.
Estas mismas propiedades de los triángulos semejantes e iguales formados por las diagonales determinan las siguientes fórmulas separadas para las diagonales del trapecio a través de los lados:
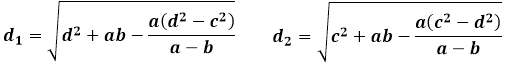
En las fórmulas dadas, la longitud de la diagonal d1 denota la diagonal del trapecio, que forma un triángulo con la base del trapecio a y el lado lateral d, y la longitud de la diagonal d2 es igual en valor, respectivamente, a la línea que conecta la base del trapecio b y el lado lateral c.
