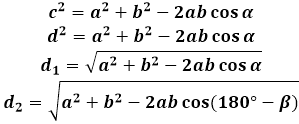Diagonales del Paralelogramo

Un paralelogramo es un cuadrilátero cuyas lados opuestos son paralelos e iguales por definición. En consecuencia, los ángulos del paralelogramo también serán iguales entre sí, y dado que la suma de todos los ángulos en un cuadrilátero es de 360 grados, se puede concluir que la suma de dos ángulos consecutivos será de 180 grados. Esta propiedad jugará un papel significativo en la búsqueda de las diagonales del paralelogramo, considerando que tienen longitudes diferentes.

Dado que cada diagonal de un paralelogramo lo divide en dos triángulos iguales, sus propiedades se utilizarán para derivar la fórmula para la diagonal de un paralelogramo.

En cualquier triángulo, el ángulo y el lado opuesto a él son proporcionales entre sí. Para un paralelogramo, esto significa que la diagonal más larga estará opuesta al ángulo obtuso, y la diagonal más corta - opuesta al ángulo agudo. Considerando que los lados de los triángulos formados por las diagonales son los mismos - estos son los lados del paralelogramo, la medida en grados del ángulo entre estos lados determina la longitud de la diagonal, calculada por la fórmula. En otras palabras, si se sustituye el valor del ángulo agudo del paralelogramo en la fórmula de la diagonal, la calculadora calculará la longitud de la diagonal corta, y si se sustituye el valor del ángulo obtuso - la larga.

Para cambiar de un ángulo a otro, se utiliza la diferencia de 180 grados y el ángulo dado, de este modo la calculadora puede calcular simultáneamente ambas diagonales.

α=180°-β

Para derivar la fórmula para la diagonal de un paralelogramo, se utiliza el teorema del coseno en el triángulo formado por la diagonal con los lados. En cualquiera de estos triángulos, la diagonal es el lado opuesto al ángulo del paralelogramo, y en consecuencia, su cuadrado es igual a la suma de los cuadrados de los otros dos lados del triángulo (del paralelogramo, en este caso) menos el doble del producto de los mismos lados por el coseno del ángulo dado. Para encontrar la longitud de la diagonal del paralelogramo, la calculadora calcula la raíz cuadrada de esta expresión.