Maatriksi transponeerimine

Transponeeritud maatriks saadakse, asendades algse maatriksi read veergudega või veerud ridadega.

Maatriksi transponeerimise omadused:
Kaks korda transponeeritud maatriks on võrdne algse maatriksigaA^TT(A^T)^T=A
Transponeeritud maatriksi summa on võrdne transponeeritud maatriksite summaga(A + B)^T=A^T+B^T
Transponeeritud maatriksi korrutis on võrdne nn transponeeritud maatriksite tegurite korrutisega, mis on võetud vastupidises järjekorras.(A × B)^T=A^T×B^T

Transponeeritud maatriksi saamiseks peate algses maatriksis sooritama ühe järgmistest toimingutest:

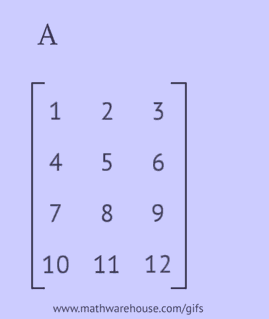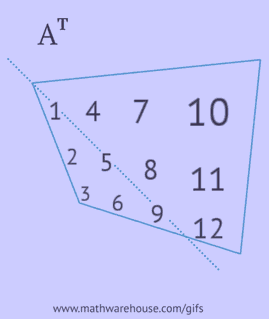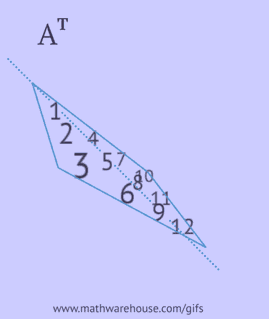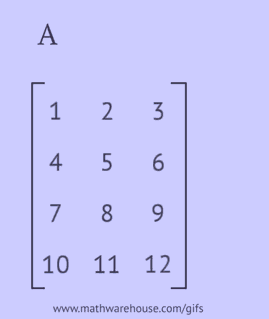
- kirjutage iga tema rida veeruna samas järjekorras;
- kirjutage iga tema veerg reana samas järjekorras;
- peegeldage tema elemente peadiagonaali suhtes, alustades ülemisest vasakust nurgast ja jätkates paremale ja alla, kuni jõutakse alumise või parema servani.

Maatriksid, mis on transponeerituks muudetud, kasutatakse algebra võrrandisüsteemide lahendamiseks, pöördmaatriksi leidmiseks ning muudeks lineaaralgebra ülesanneteks.