Breuken
Wat is een breuk?
Breuk in de wiskunde — een getal bestaande uit één of meerdere delen (delen) van een eenheid.
Volgens de schrijfwijze worden breuken ingedeeld in twee formaten: gewone van de vorm 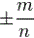 , en decimale.
, en decimale.
Soorten breuken:
Gewone breuken
Gewone breuk (eenvoudige) heeft de vorm, waarbij m en n - natuurlijke getallen zijn.
Teller (m)- wordt de teller van de breuk genoemd, noemer (n) - wordt de noemer van deze breuk genoemd.
De horizontale of schuine lijn in een breuk duidt op deling.
Belangrijk!
In elke breuk, zowel in juiste als onjuiste n is de noemer niet nul, aangezien delen door nul niet is toegestaan.
Voorbeelden van gewone breuken: 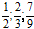
Juiste breuken
Een breuk wordt juist genoemd als de absolute waarde van de teller kleiner is dan de absolute waarde van de noemer.
Voorbeelden van juiste breuken: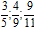
Berekeningen en formules van breuken online
calculator voor het oplossen van breuken | bereken de som |
vind de som van breuken | vind het product van breuken |
bereken het quotiënt van breuken | Bereken directe en omgekeerde evenredigheid |
hoe een breuk tot een macht te verheffen | hoe een breuk te vergelijken |
zet een gewone breuk om | Effectieve oplossing voor werken met verhoudingen |
zet om naar een onjuiste breuk | omzetting van een onjuiste breuk naar een gemengde breuk |
Onjuiste breuken
Een breuk wordt onjuist genoemd als de absolute waarde van de teller groter is dan de absolute waarde van de noemer.
Voorbeelden van onjuiste breuken: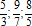
Gemengde getallen
De weergave van een getal dat een geheel en een breukdeel bevat, wordt een gemengd getal genoemd.
Een gemengd getal kan worden weergegeven als een onjuiste breuk.
Voorbeelden van gemengde getallen: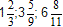
Decimale breuken
Er zijn taken waarbij de omzetting van een gewone breuk naar een decimale gewoonweg noodzakelijk is.
Een decimale breuk is een breuk die zonder noemer wordt geschreven.
U kunt de omzetting van een gewone breuk naar een decimale hier
Voorbeelden van decimale breuken:
0,1; 0,13; 0,121.
