Addition av bråk
Addition av bråk med samma nämnare:
Definition: Summan av bråk med samma nämnare kallas en bråkdel vars täljare är lika med summan av täljarna av de ursprungliga bråken, med en nämnare som är lika med nämnaren för båda bråken.Formel
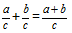
Låt oss addera två bråk med samma nämnare
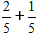
Enligt formeln adderar vi täljarna, och behåller nämnaren densamma
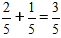
Viktigt: Om möjligt, skriver vi den förenklade bråkdelen i slutsvaret.
Exempel:
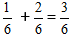När vi förenklar bråkdelen, får vi numret 1/2 Addition av bråk med olika nämnare:
Definition: För att hitta summan av bråk med olika nämnare, först för bråken till en gemensam nämnare, och sedan addera dem som bråk med samma nämnare.Uppgift:
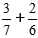
Lösningsprocess:
1) Vi för bråken till en gemensam nämnare.
För att göra detta, hittar vi MGM - Minsta gemensamma multipel, för nämnarna 7 och 6, är detta nummer 42.
Dela numret 42 med nämnarna av bråken 3/7 och 2/6
Således, hittade vi de ytterligare multiplikatorerna.
Nästa, multiplicera bråken med de ytterligare multiplikatorerna och få uttrycket:
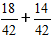
2) Addera bråken.
I vårt fall kan bråkdelen förenklas med 2, och i slutsvaret skriver vi numret 16/21
Addition av en bråkdel och ett heltal:
Definition: För att addera en bråkdel till ett heltal, representera först heltalet som en bråkdel med en nämnare lika med 1.Beräkningsalgoritm:
1) Vi för bråken till en gemensam nämnare.
2) Addera bråken
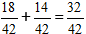
3) Om möjligt, förenkla den resulterande bråkdelen.
4) Om resultatet är en oäkta bråkdel, beräkna hela delen från den.
Exempel:
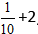
Lösning:
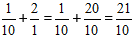
Beräkna hela delen, och få svaret
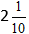
Addition av blandade bråk:
Definition: För att addera blandade bråk behöver du separat addera hela delarna, och separat de bråkdelarna.Formel
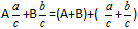
Exempel:
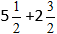
Sätt in talen i formeln:
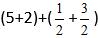
Vi får:
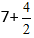
Från bråkdelen, beräkna hela delen eftersom den är oäkta, och få uttrycket 7+2=9.