การทรานสโพสเมทริกซ์
เมทริกซ์ที่ทรานสโพสคือเมทริกซ์ที่ได้จากการแทนที่แถวของเมทริกซ์เดิมด้วยคอลัมน์หรือคอลัมน์ด้วยแถว
คุณสมบัติของการทรานสโพสเมทริกซ์:เมทริกซ์ที่ทรานสโพสสองครั้งเท่ากับเมทริกซ์เดิมATT(AT)T=A
เมทริกซ์ที่ทรานสโพสของผลรวมเท่ากับผลรวมของเมทริกซ์ที่ทรานสโพส(A + B)T=AT+BT
เมทริกซ์ที่ทรานสโพสของผลคูณเท่ากับผลคูณของเมทริกซ์ที่ทรานสโพสของตัวประกอบ, ที่ถูกนำในการย้อนกลับ(A × B)T=AT×BT
ในการได้เมทริกซ์ที่ทรานสโพส, คุณต้องดำเนินการขั้นตอนหนึ่งในดังต่อไปนี้กับเมทริกซ์เดิม:
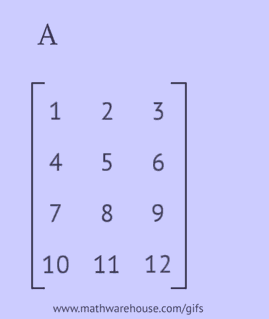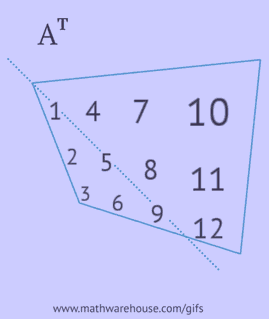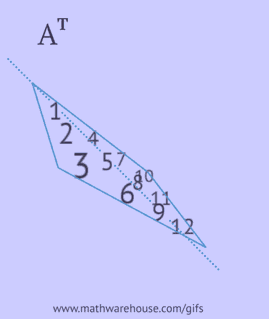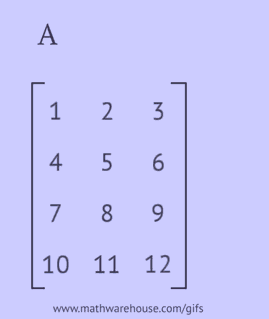
- บันทึกแต่ละแถวของมันเป็นคอลัมน์ในลำดับเดียวกัน;
- บันทึกแต่ละคอลัมน์ของมันเป็นแถวในลำดับเดียวกัน;
- สะท้อนองค์ประกอบของมันเทียบกับแนวทแยงหลัก, เริ่มจากมุมบนซ้ายและดำเนินต่อไปทางขวาและลงจนถึงขอบล่างหรือขวา
เมทริกซ์ที่เปลี่ยนเป็นทรานสโพสถูกใช้ในการแก้ระบบสมการเชิงพีชคณิต, การหามิทริกซ์ผกผัน, รวมถึงในงานอื่นๆ ของพีชคณิตเชิงเส้น
