Addition af Brøker
Addition af Brøker med Samme Nævnere:
Definition: Summen af brøker med samme nævnere kaldes en brøk, hvis tæller er lig med summen af tællerne i de oprindelige brøker, med en nævner lig med nævneren af begge brøker.Formel
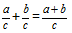
Lad os lægge to brøker sammen med samme nævnere
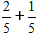
Ifølge formlen lægger vi tællerne sammen og holder nævneren den samme
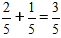
Vigtigt: Hvis det er muligt, skriver vi den forenklede brøk i det endelige svar.
Eksempel:
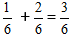Ved forenkling af brøken får vi tallet 1/2 Addition af Brøker med Forskellige Nævnere:
Definition: For at finde summen af brøker med forskellige nævnere, bringes brøkerne først til en fælles nævner, og derefter lægges de sammen som brøker med samme nævnere.Opgave:
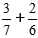
Løsningsproces:
1) Vi bringer brøkerne til en fælles nævner.
For at gøre dette finder vi MFM - Mindste Fælles Multipel, for nævnerne 7 og 6, er dette tal 42.
Divider tallet 42 med nævnerne af brøkerne 3/7 og 2/6
Således fandt vi de ekstra multiplikatorer.
Derefter multiplicerer vi brøkerne med de ekstra multiplikatorer og får udtrykket:
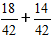
2) Læg brøkerne sammen.
I vores tilfælde kan brøken forenkles med 2, og i det endelige svar skriver vi tallet 16/21
Addition af en Brøk og et Heltal:
Definition: For at lægge en brøk til et heltal repræsenteres hele tallet først som en brøk med en nævner lig med 1.Beregning Algoritme:
1) Vi bringer brøkerne til en fælles nævner.
2) Læg brøkerne sammen
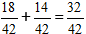
3) Hvis det er muligt, forenkl den resulterende brøk.
4) Hvis resultatet er en uægte brøk, beregn den hele del fra den.
Eksempel:
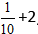
Løsning:
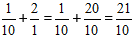
Beregn den hele del, og få svaret
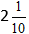
Addition af Blandet Brøker:
Definition: For at lægge blandede brøker skal du separat lægge de hele dele sammen, og separat de brøkdele.Formel
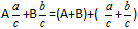
Eksempel:
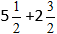
Indsæt tallene i formlen:
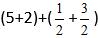
Vi får:
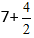
Fra brøken beregner vi den hele del, da den er uægte, og får udtrykket 7+2=9.