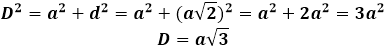Diagonal del Cubo

Un cubo es un cuerpo geométrico básico cuando se trata de volumen y cuerpos volumétricos. No es sorprendente que la tercera potencia, que se obtiene multiplicando tres números idénticos entre sí (como al encontrar el volumen de un cubo - tres de sus medidas idénticas) es nombrada en su honor.

El parámetro principal y único del cubo es su arista a, ya que todas las aristas de un cubo son congruentes y representan tanto longitud, ancho y altura. En consecuencia, solo un valor determina todas las características posibles del cubo relacionadas con sus dimensiones.

Además de las aristas, los vértices del cubo pueden conectarse mediante diagonales. Las diagonales pueden pasar a través de las caras del cubo, en cuyo caso simplemente serán la diagonal de la base o la diagonal del cuadrado en el plano, o las diagonales pueden dibujarse dentro del cubo mismo, conectando bases opuestas en puntos extremos (vértices).

Para encontrar la diagonal del cubo a través de su arista, primero necesita hacer una construcción adicional en forma de la diagonal de una de las bases conectadas, luego la diagonal del cubo se convierte en la hipotenusa del triángulo rectángulo recién formado, cuyos catetos son la arista del cubo y la diagonal de la base. Si la arista del cubo está dada por las condiciones del problema, entonces la diagonal del cuadrado en la base debe primero calcularse usando la fórmula: d=a√2

Entonces la diagonal del cubo puede expresarse a través de el teorema de Pitágoras, y tomará la siguiente forma: