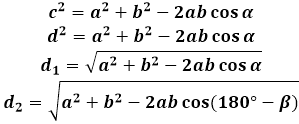평행사변형 대각선

평행사변형은 그 정의에 따라 마주보는 변이 평행하고 같은 사각형입니다. 따라서, 마주보는 평행사변형의 각도 또한 서로 같을 것이며, 사각형의 모든 각도의 합이 360도이므로, 연속하는 두 각의 합이 180도임을 알 수 있습니다. 이 성질은 평행사변형의 대각선을 찾는 데 중요한 역할을 하며, 대각선이 길이가 다르다는 점을 고려합니다.

각 평행사변형의 대각선은 두 개의 동일한 삼각형으로 나뉘어지므로, 그들의 성질을 사용하여 평행사변형의 대각선 공식을 도출할 것입니다.

모든 삼각형에서, 각과 그에 대립하는 변은 서로 비례합니다. 평행사변형의 경우, 긴 대각선은 둔각에 대립하고, 짧은 대각선은 예각에 대립합니다. 대각선에 의해 형성된 삼각형의 변이 동일하다는 점을 고려하면, 이는 평행사변형의 변이며, 이 변 사이의 각도의 도수는 공식을 통해 길이를 결정합니다. 즉, 평행사변형의 예각 값을 대각선 공식에 대입하면, 계산기는 짧은 대각선의 길이를 계산하고, 둔각 값을 대입하면 긴 대각선의 길이를 계산합니다.

한 각도에서 다른 각도로 전환하기 위해 180도와 주어진 각도의 차이를 사용하여, 계산기는 두 대각선을 동시에 계산할 수 있습니다.

α=180°-β

평행사변형의 대각선 공식을 유도하기 위해, 대각선과 변에 의해 형성된 삼각형에서 코사인 정리가 사용됩니다. 이러한 삼각형 중 어느 하나에서, 대각선은 평행사변형의 각에 대립하는 변이며, 그 제곱은 삼각형의 다른 두 변의 제곱합과 같습니다 (평행사변형의 변, 이 경우) 주어진 각도의 코사인에 의해 같은 변의 두 배의 곱을 뺀 값입니다. 평행사변형의 대각선 길이를 찾기 위해, 계산기는 이 표현식의 제곱근을 계산합니다.