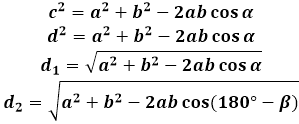Parallelogram Diagonals

A parallelogram is a quadrilateral whose opposite sides are parallel and equal by definition. Consequently, the opposite angles of the parallelogram will also be equal to each other, and since the sum of all angles in a quadrilateral is 360 degrees, it can be concluded that the sum of two consecutive angles will be 180 degrees. This property will play a significant role in finding the diagonals of the parallelogram, considering that they are of different lengths.

Since each diagonal of a parallelogram divides it into two equal triangles, their properties will be used to derive the formula for the diagonal of a parallelogram.

In any triangle, the angle and the side opposite to it are proportional to each other. For a parallelogram, this means that the longer diagonal will lie opposite the obtuse angle, and the shorter diagonal - opposite the acute angle. Considering that the sides of the triangles formed by the diagonals are the same - these are the sides of the parallelogram, the degree measure of the angle between these sides determines the length of the diagonal, calculated by the formula. In other words, if the value of the acute angle of the parallelogram is substituted into the formula for the diagonal, the calculator will calculate the length of the short diagonal, and if the value of the obtuse angle is substituted - the long one.

To switch from one angle to another, the difference of 180 degrees and the given angle is used, thus the calculator can simultaneously calculate both diagonals.

α=180°-β

To derive the formula for the diagonal of a parallelogram, the cosine theorem in the triangle formed by the diagonal with the sides is used. In any of such triangles, the diagonal is the side opposite the parallelogram's angle, and accordingly, its square equals the sum of squares of the two other sides of the triangle (of the parallelogram, in this case) minus twice the product of the same sides by the cosine of the given angle. To find the length of the diagonal of the parallelogram, the calculator calculates the square root of this expression.