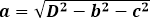Rectangular Parallelepiped Diagonal

A parallelepiped is a particular case of a prism, at the base of which lies a rectangle with length a and width b. Moving along the vertical or inclined axis to a certain height c, this rectangle creates a volumetric body called a parallelepiped.

By definition, a parallelepiped can be inclined or straight, meaning the angle between the height and the rectangle at the base varies from 0 to 90 degrees. A straight parallelepiped has exclusively rectangular faces, and sometimes even a square (at the base), therefore solving problems involving it is significantly simplified. In the case of an inclined parallelepiped, the formulas must take into account that the lateral face is a parallelogram, whose construction also depends on its angle of inclination.

In addition to the three aforementioned parameters of the parallelepiped - length, width, and height, which are its edges, several more segments can be drawn connecting its vertices. As in geometric figures on the plane, lines passing inside the main frame through vertices are called diagonals. The diagonals of the lateral faces of a rectangular parallelepiped are identical to the diagonals of the rectangles that represent the faces - they can, therefore, be calculated using a suitable online calculator for rectangles.

Another matter is the diagonal that does not pass on the outer surface of the rectangular parallelepiped but through it, connecting opposite vertices of the upper and lower bases. In this case, which particular pair of opposite vertices is connected does not matter for calculations, since if you consider sections, you can see that both diagonals of the parallelepiped are identical and can be found in the same way.

So, to derive the formula for the diagonal through length, width, and height, it is necessary to enclose the diagonal in a flat geometric figure, whose properties can be used. For this, in any base - upper or lower, a diagonal is drawn, which forms with the parallelepiped diagonal and the side edge (height) right triangle. Applying only the Pythagorean theorem, you can find the base diagonal through width and length, and then the rectangular parallelepiped diagonal, adding height to the calculations.

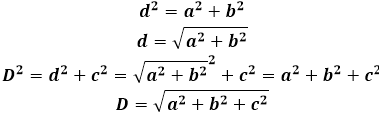
Using the last and the penultimate formula, you can also successfully find the length, width, or height of a rectangular parallelepiped, having three out of four parameters, including the parallelepiped diagonal, in the given conditions. For example: