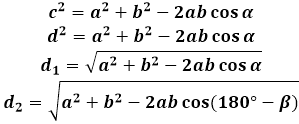Diagonais do Paralelogramo
Um paralelogramo é um quadrilátero cujos lados opostos são paralelos e iguais por definição. Consequentemente, os ângulos do paralelogramo também serão iguais entre si, e como a soma de todos os ângulos em um quadrilátero é 360 graus, pode-se concluir que a soma de dois ângulos consecutivos será de 180 graus. Esta propriedade desempenhará um papel significativo na determinação das diagonais do paralelogramo, considerando que possuem comprimentos diferentes.
Como cada diagonal de um paralelogramo a divide em dois triângulos iguais, suas propriedades serão usadas para derivar a fórmula para a diagonal de um paralelogramo.
Em qualquer triângulo, o ângulo e o lado oposto a ele são proporcionais um ao outro. Para um paralelogramo, isso significa que a diagonal mais longa ficará oposta ao ângulo obtuso, e a diagonal mais curta - oposta ao ângulo agudo. Considerando que os lados dos triângulos formados pelas diagonais são os mesmos - esses são os lados do paralelogramo, a medida em graus do ângulo entre esses lados determina o comprimento da diagonal, calculado pela fórmula. Em outras palavras, se o valor do ângulo agudo do paralelogramo for substituído na fórmula da diagonal, a calculadora calculará o comprimento da diagonal curta, e se o valor do ângulo obtuso for substituído - a longa.
Para alternar de um ângulo para outro, é utilizada a diferença de 180 graus e o ângulo dado, assim a calculadora pode calcular simultaneamente ambas as diagonais.
α=180°-β
Para derivar a fórmula para a diagonal de um paralelogramo, é usado o teorema do cosseno no triângulo formado pela diagonal com os lados. Em qualquer um desses triângulos, a diagonal é o lado oposto ao ângulo do paralelogramo e, consequentemente, seu quadrado é igual à soma dos quadrados dos outros dois lados do triângulo (do paralelogramo, neste caso) menos duas vezes o produto dos mesmos lados pelo cosseno do ângulo dado. Para encontrar o comprimento da diagonal do paralelogramo, a calculadora calcula a raiz quadrada dessa expressão.