Adunarea fracțiunilor
Adunarea fracțiunilor cu aceiași numitori:
Definiție: Suma fracțiunilor cu aceiași numitori se numește fracțiune al cărei numărător este egal cu suma numărătorilor fracțiunilor originale, cu un numitor egal cu numitorul ambelor fracțiuni.Formulă
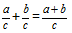
Să adunăm două fracțiuni cu aceiași numitori
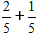
Conform formulei, adunăm numărătorii și păstrăm numitorul același
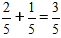
Important: Dacă este posibil, scriem fracțiunea simplificată în răspunsul final.
Exemplu:
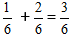Când simplificăm fracțiunea, obținem numărul 1/2 Adunarea fracțiunilor cu numitori diferiți:
Definiție: Pentru a găsi suma fracțiunilor cu numitori diferiți, mai întâi aducem fracțiunile la un numitor comun, apoi le adunăm ca fracțiuni cu aceiași numitori.Sarcină:
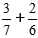
Procesul de soluționare:
1) Aducem fracțiunile la un numitor comun.
Pentru aceasta, găsim CMF - Cel Mai Mic Multiplu Comun, pentru numitorii 7 și 6, acest număr este 42.
Împărțim numărul 42 la numitorii fracțiunilor 3/7 și 2/6
Astfel, am găsit multiplicatorii suplimentari.
Apoi, înmulțim fracțiunile cu multiplicatorii suplimentari și obținem expresia:
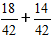
2) Adăugăm fracțiunile.
În cazul nostru, fracțiunea poate fi simplificată prin 2, și în răspunsul final scriem numărul 16/21
Adunarea unei fracțiuni și a unui număr întreg:
Definiție: Pentru a adăuga o fracțiune la un număr întreg, mai întâi reprezentăm numărul întreg ca o fracțiune cu un numitor egal cu 1.Algoritmul de calcul:
1) Aducem fracțiunile la un numitor comun.
2) Adăugăm fracțiunile
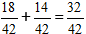
3) Dacă este posibil, simplificăm fracțiunea rezultată.
4) Dacă rezultatul este o fracțiune improprie, calculăm partea întreagă din aceasta.
Exemplu:
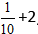
Soluție:
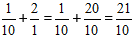
Calculăm partea întreagă și obținem răspunsul
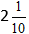
Adunarea fracțiunilor mixte:
Definiție: Pentru a adăuga fracțiuni mixte trebuie să adăugăm separat părțile întregi și separat părțile fracționare.Formulă
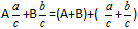
Exemplu:
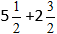
Substituim numerele în formulă:
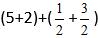
Obținem:
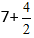
Din fracțiune, calculăm partea întreagă deoarece este improprie și obținem expresia 7+2=9.