Диагонали на трапеца
Трапец е неконвенционален четириъгълник, в който две от страните – основите на трапеца, са паралелни една на друга. Ако начертаете диагонали в трапец, те образуват серия от подобни триъгълници и пропорционалните отношения на техните страни водят до основното свойство на трапеца, свързващо диагоналите на трапеца и неговите четири страни:
d12+d22=c2+d2+2ab , където a и b – това са основите на трапеца, и c и d – неговите странични страни.
Същите свойства на подобните и равни триъгълници, образувани от диагоналите, определят следните отделни формули за диагоналите на трапеца чрез страните:
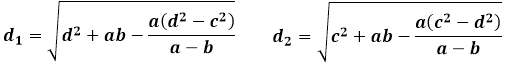
В дадените формули, дължината на диагонала d1 обозначава диагонала на трапеца, който образува триъгълник с основата на трапеца a и страничната страна d, и дължината на диагонала d2 е равна по стойност, съответно, на линията, свързваща основата на трапеца b и страничната страна c.
