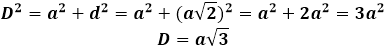Диагонал на куба

Кубът е основно геометрично тяло, когато става въпрос за обем и обемни тела. Не е изненадващо, че третата степен, която се получава чрез умножение на три идентични числа едно с друго (както при намирането на обема на куб - три от неговите идентични измерения) носи името му.

Основният и единствен параметър на куба е неговото ребро a, тъй като всички ребра на куба са конгруентни и представляват както дължина, ширина, така и височина. Съответно, само една стойност определя всички възможни характеристики на куба, свързани с неговите размери.

Освен ребрата, върховете на куба могат да бъдат свързани с диагонали. Диагоналите могат да преминават през лицата на куба, в който случай те просто ще бъдат диагонал на основата или диагонал на квадрата в равнината, или диагоналите могат да бъдат начертани вътре в самия куб, свързвайки противоположни основи в крайните точки (върховете).

За да намерите диагонала на куб чрез неговото ребро, първо трябва да направите допълнителна конструкция във формата на диагонала на една от свързаните основи, след което диагоналът на куба става хипотенуза на новосформирания правоъгълен триъгълник, чиито катети са реброто на куба и диагоналът на основата. Ако реброто на куба е дадено от условията на задачата, тогава диагоналът на квадрата в основата трябва първо да бъде изчислен с помощта на формулата: d=a√2

Тогава диагоналът на куба може да бъде изразен чрез теоремата на Питагор, и тя ще приеме следната форма: