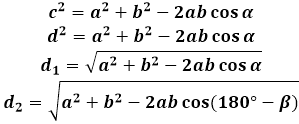Диагонали на успоредника

Паралелограмът е четириъгълник, чиито противоположни страни са паралелни и равни по дефиниция. Следователно, противоположните ъгли на паралелограма също ще бъдат равни един на друг и тъй като сумата на всички ъгли в четириъгълник е 360 градуса, може да се заключи, че сумата на два последователни ъгъла ще бъде 180 градуса. Това свойство ще играе значителна роля при намирането на диагоналите на паралелограма, като се има предвид, че те са с различна дължина.

Тъй като всеки диагонал на паралелограм го разделя на два равни триъгълника, техните свойства ще бъдат използвани за извеждане на формулата за диагонала на паралелограм.

Във всеки триъгълник ъгълът и страната, противоположна на него, са пропорционални един на друг. За паралелограм това означава, че по-дългият диагонал ще лежи срещу тъпия ъгъл, а по-късият диагонал - срещу острия ъгъл. Като се има предвид, че страните на триъгълниците, образувани от диагоналите, са същите - това са страните на паралелограма, степенната мярка на ъгъла между тези страни определя дължината на диагонала, изчислена по формулата. С други думи, ако стойността на острия ъгъл на паралелограма бъде заместена във формулата за диагонал, калкулаторът ще изчисли дължината на късия диагонал, а ако стойността на тъпия ъгъл бъде заместена - дългия.

За да преминете от един ъгъл към друг, се използва разликата от 180 градуса и дадения ъгъл, така че калкулаторът може едновременно да изчисли и двата диагонала.

α=180°-β

За да се изведе формулата за диагонала на паралелограм, се използва теоремата на косинусите в триъгълника, образуван от диагонала със страните. Във всеки от тези триъгълници диагоналът е страната, противоположна на ъгъла на паралелограма и следователно, неговият квадрат е равен на сумата от квадратите на другите две страни на триъгълника (на паралелограма, в този случай) минус двойния продукт на същите страни по косинуса на дадения ъгъл. За да се намери дължината на диагонала на паралелограм, калкулаторът изчислява квадратния корен на това изразяване.