Sčítání zlomků
Sčítání zlomků se stejnými jmenovateli:
Definice: Součtem zlomků se stejnými jmenovateli je nazýván zlomek, jehož čitatel je roven součtu čitatelů původních zlomků a jmenovatel je roven jmenovateli obou zlomků.Vzorec
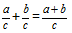
Sečtěme dva zlomky se stejnými jmenovateli
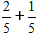
Podle vzorce sečteme čitatele a jmenovatele ponecháme stejné
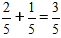
Důležité: Pokud je to možné, zapíšeme zjednodušený zlomek ve finální odpovědi.
Příklad:
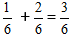 Při zjednodušování zlomku dostaneme číslo 1/2
Při zjednodušování zlomku dostaneme číslo 1/2 Sčítání zlomků s různými jmenovateli:
Definice: Abychom našli součet zlomků s různými jmenovateli, nejprve přivedeme zlomky na společný jmenovatel a pak je sečteme jako zlomky se stejnými jmenovateli.Úkol:
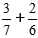
Postup řešení:
1) Přivedeme zlomky na společný jmenovatel.
K tomu najdeme NSN - Nejmenší společný násobek, pro jmenovatele 7 a 6, toto číslo je 42.
Dělíme číslo 42 jmenovateli zlomků 3/7 a 2/6
Tak jsme našli doplňkové násobitele.
Dále násobíme zlomky doplňkovými násobiteli a dostaneme výraz:
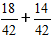
2) Sečteme zlomky.
V našem případě lze zlomek zjednodušit číslem 2 a ve finální odpovědi zapíšeme číslo 16/21
Sčítání zlomku a celého čísla:
Definice: Abychom přidali zlomek k celému číslu, nejprve reprezentujeme celé číslo jako zlomek s jmenovatelem rovným 1.Algoritmus výpočtu:
1) Přivedeme zlomky na společný jmenovatel.
2) Sečteme zlomky
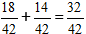
3) Pokud je to možné, zjednodušíme výsledný zlomek.
4) Pokud je výsledkem nepravý zlomek, vypočítáme z něj celou část.
Příklad:
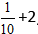
Řešení:
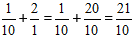
Vypočítáme celou část a dostaneme odpověď
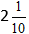
Sčítání smíšených zlomků:
Definice: Abychom sečetli smíšené zlomky je třeba jednotlivě sečíst celé části a jednotlivě sečíst část zlomkovou.Vzorec
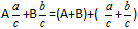
Příklad:
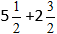
Dosadíme čísla do vzorce:
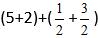
Získáme:
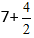
Ze zlomku vypočítáme celou část, protože je nepravý, a dostaneme výraz 7+2=9.
