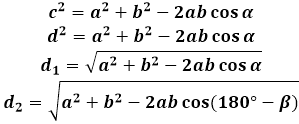Úhlopříčky rovnoběžníku

Rovnoběžník je čtyřúhelník, jehož protější strany jsou rovnoběžné a shodné podle definice. Následkem toho jsou protější úhly rovnoběžníku také stejné k sobě, a protože součet všech úhlů v čtyřúhelníku je 360 stupňů, lze dojít k závěru, že součet dvou po sobě jdoucích úhlů bude 180 stupňů. Tato vlastnost bude hrát významnou roli při hledání diagonál rovnoběžníku, s přihlédnutím k tomu, že jsou různé délky.

Protože každá diagonála rovnoběžníku ho dělí na dva stejné trojúhelníky, jejich vlastnosti budou použity k odvození vzorce pro diagonálu rovnoběžníku.

V jakémkoli trojúhelníku jsou úhel a protější strana k sobě úměrné. Pro rovnoběžník to znamená, že delší diagonála bude ležet naproti tupému úhlu a kratší diagonála - naproti ostrému úhlu. S přihlédnutím k tomu, že strany trojúhelníků tvořených diagonálami jsou stejné - to jsou strany rovnoběžníku, stupňová míra úhlu mezi těmito stranami určuje délku diagonály, vypočítanou podle vzorce. Jinými slovy, pokud se hodnota ostrého úhlu rovnoběžníku dosadí do vzorce pro diagonálu, kalkulátor vypočítá délku krátké diagonály, a pokud se dosadí hodnota tupého úhlu - dlouhé.

Pro přechod z jednoho úhlu na druhý se používá rozdíl 180 stupňů a daný úhel, čímž kalkulátor může současně vypočítat obě diagonály.

α=180°-β

K odvození vzorce pro diagonálu rovnoběžníku se používá kosinová věta v trojúhelníku tvořeném diagonálou se stranami. V jakémkoli takovém trojúhelníku je diagonála stranou naproti úhlu rovnoběžníku a odpovídajícím způsobem její čtverec se rovná součtu čtverců dvou dalších stran trojúhelníku (roznoběžníku, v tomto případě) mínus dvakrát součin stejných stran s kosinem daného úhlu. Pro nalezení délky diagonály rovnoběžníku kalkulátor vypočítá druhou odmocninu tohoto výrazu.