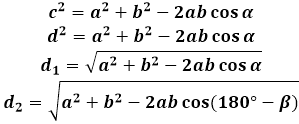Parallelogrammets Diagonaler

Et parallelogram er en firkant, hvis modsatte sider er parallelle og ens per definition. Følgelig vil de modsatte vinkler i parallelogrammet vil også være lige med hinanden, og da summen af alle vinkler i en firkant er 360 grader, kan det konkluderes, at summen af to på hinanden følgende vinkler vil være 180 grader. Denne egenskab vil spille en væsentlig rolle i at finde diagonalerne i parallelogrammet, idet de er af forskellig længde.

Da hver diagonal i et parallelogram deler det i to lige store trekanter, vil deres egenskaber blive brugt til at udlede formlen for diagonalen i et parallelogram.

I enhver trekant er vinklen og den modsatte side proportionale med hinanden. For et parallelogram betyder det, at den længere diagonal vil ligge modsat den stumpe vinkel, og den kortere diagonal - modsat den spidse vinkel. Da siderne af de trekanter, der dannes af diagonalerne, er de samme - disse er parallelogrammets sider, vil gradmålingen af vinklen mellem disse sider bestemme længden af diagonalen, beregnet ved formlen. Med andre ord, hvis værdien af den spidse vinkel i parallelogrammet indsættes i formlen for diagonalen, vil beregneren beregne længden af den korte diagonal, og hvis værdien af den stumpe vinkel indsættes - den lange.

For at skifte fra en vinkel til en anden anvendes forskellen på 180 grader og den givne vinkel, således at beregneren samtidig kan beregne begge diagonaler.

α=180°-β

For at udlede formlen for diagonalen i et parallelogram anvendes cosinus-sætningen i trekanten dannet af diagonalen med siderne. I nogen af sådanne trekanter er diagonalen siden modsat parallelogrammets vinkel, og henholdsvis er dens kvadrat lig summen af kvadraterne på de to andre sider af trekanten (af parallelogrammet, i dette tilfælde) minus det dobbelte af produktet af de samme sider med cosinus af den givne vinkel. For at finde længden af diagonalen i parallelogrammet beregner beregneren kvadratroden af dette udtryk.