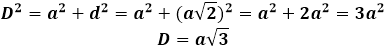Kube Diagonal

En kube er et grundlæggende geometrisk legeme, når det kommer til volumen og rumlige legemer. Ikke overraskende er den tredje potens, som opnås ved at multiplicere tre identiske tal sammen (som når man finder volumen af en kube - tre af dens identiske målinger) er navngivet i dens ære.

Den primære og eneste parameter for kuben er dens kant a, da alle kanter af en kube er kongruente og repræsenterer både længde, bredde og højde. Tilsvarende bestemmer kun én værdi alle mulige egenskaber ved kuben relateret til dens dimensioner.

Ud over kanterne kan kubens hjørner forbindes med diagonaler. Diagonaler kan passere gennem kubens flader, i hvilket tilfælde de blot vil være basisdiagonalen eller kvadratdiagonalen i planet, eller diagonalerne kan tegnes inde i selve kuben, der forbinder modsatte baser ved ekstreme punkter (toppunkter).

For at finde kubens diagonal gennem sin kant, skal du først lave en ekstra konstruktion i form af diagonalen af en af de forbundne baser, derefter bliver kubens diagonal hypotenusen af den nyoprettede retvinklede trekant, hvis ben er kubens kant og basisdiagonalen. Hvis kanten af kuben er givet ved opgavens betingelser, skal kvadratdiagonalen ved basen først beregnes ved hjælp af formlen: d=a√2

Så kan kubens diagonal udtrykkes gennem Pythagoras' sætning, og den vil tage følgende form: