Trapezdiagonalen

Ein Trapez ist ein unkonventionelles Viereck, in dem zwei der Seiten – die Basen des Trapezes, parallel zueinander sind. Wenn Sie Diagonalen in einem Trapez zeichnen, bilden sie eine Reihe ähnlicher Dreiecke, und die proportionalen Beziehungen ihrer Seiten führen zur Haupteigenschaft des Trapezes, die die Diagonalen des Trapezes und seine vier Seiten kombiniert:
d₁²+d₂²=c²+d²+2ab , wo a und b – das sind die Basen des Trapezes, und c und d – seine Seiten.

Diese gleichen Eigenschaften der ähnlichen und gleichwertigen Dreiecke, die durch die Diagonalen gebildet werden, bestimmen die folgenden separaten Formeln für die Trapezdiagonalen durch die Seiten:

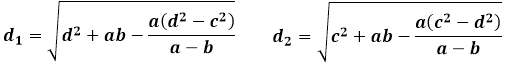
In den angegebenen Formeln ist die Länge der Diagonale d₁ bezeichnet die Diagonale des Trapezes, die ein Dreieck mit der Basis des Trapezes bildet a und der Seiten d, und die Länge der Diagonale d₂ ist im Wert gleich der Linie, die die Basis des Trapezes verbindet b und die Seiten c.