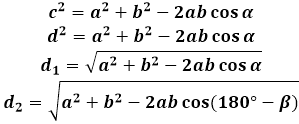Parallelogrammdiagonalen
Ein Parallelogramm ist ein Viereck, dessen gegenüberliegende Seiten parallel und per Definition gleich sind. Folglich sind die gegenüberliegenden Winkel des Parallelogramms werden ebenfalls gleich zueinander sein, und da die Summe aller Winkel in einem Viereck 360 Grad beträgt, kann daraus geschlossen werden, dass die Summe von zwei aufeinanderfolgenden Winkeln 180 Grad beträgt. Diese Eigenschaft wird eine bedeutende Rolle beim Finden der Diagonalen des Parallelogramms spielen, da sie unterschiedliche Längen haben.
Da jede Diagonale eines Parallelogramms es in zwei gleiche Dreiecke teilt, werden ihre Eigenschaften verwendet, um die Formel für die Diagonale eines Parallelogramms abzuleiten.
In jedem Dreieck stehen der Winkel und die gegenüberliegende Seite in einem Verhältnis zueinander. Für ein Parallelogramm bedeutet dies, dass die längere Diagonale gegenüber dem stumpfen Winkel liegt, und die kürzere Diagonale - gegenüber dem spitzen Winkel. Da die Seiten der durch die Diagonalen gebildeten Dreiecke dieselben sind - das sind die Seiten des Parallelogramms, bestimmt das Maß des Winkels zwischen diesen Seiten die Länge der Diagonale, berechnet durch die Formel. Mit anderen Worten, wenn der Wert des spitzen Winkels des Parallelogramms in die Formel für die Diagonale eingesetzt wird, berechnet der Rechner die Länge der kurzen Diagonale, und wenn der Wert des stumpfen Winkels eingesetzt wird - die lange.
Um von einem Winkel zum anderen zu wechseln, wird die Differenz von 180 Grad und dem gegebenen Winkel verwendet, so dass der Rechner gleichzeitig beide Diagonalen berechnen kann.
α=180°-β
Um die Formel für die Diagonale eines Parallelogramms abzuleiten, wird der Kosinussatz im durch die Diagonale mit den Seiten gebildeten Dreieck verwendet. In jedem dieser Dreiecke ist die Diagonale die Seite gegenüber dem Winkel des Parallelogramms, und entsprechend ist ihr Quadrat gleich der Summe der Quadrate der beiden anderen Seiten des Dreiecks (des Parallelogramms, in diesem Fall) minus zweimal das Produkt der gleichen Seiten durch den Kosinus des gegebenen Winkels. Um die Länge der Diagonale des Parallelogramms zu finden, berechnet der Rechner die Quadratwurzel aus diesem Ausdruck.