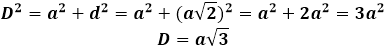Würfeldiagonale

Ein Würfel ist ein grundlegender geometrischer Körper, wenn es um Volumen und volumetrische Körper geht. Kein Wunder, dass die dritte Potenz, die durch die Multiplikation von drei gleichen Zahlen entsteht (wie beim Finden des Volumens eines Würfels - drei seiner identischen Maße) ihm zu Ehren benannt ist.

Der Haupt- und einzige Parameter des Würfels ist seine Kante a, da alle Kanten eines Würfels kongruent sind und sowohl Länge, Breite als auch Höhe darstellen. Dementsprechend bestimmt ein einziger Wert alle möglichen Eigenschaften des Würfels, die mit seinen Abmessungen zusammenhängen.

Zusätzlich zu den Kanten können die Würfelspitzen durch Diagonalen verbunden werden. Diagonalen können durch die Würfelflächen verlaufen, in diesem Fall sind sie einfach die Basisdiagonale oder die Quadratdiagonale in der Ebene, oder die Diagonalen können im Würfel selbst gezeichnet werden, wobei sie gegenüberliegende Basen an Extrempunkten verbinden (Gipfeln).

Um die Würfeldiagonale über seine Kante zu finden, müssen Sie zunächst eine zusätzliche Konstruktion in Form der Diagonale einer der verbundenen Basen vornehmen, dann wird die Würfeldiagonale zur Hypotenuse des neu gebildeten rechtwinkligen Dreiecks, dessen Katheten die Kante des Würfels und die Basisdiagonale sind. Wenn die Kante des Würfels durch die Bedingungen des Problems gegeben ist, muss die Quadratdiagonale an der Basis zuerst mit der Formel berechnet werden: d=a√2

Dann kann die Würfeldiagonale durch den Satz des Pythagoras, und sie wird folgende Form annehmen: