Διαγώνιοι Τραπέζιου
Ένα τραπέζιο είναι ένα μη συμβατικό τετράπλευρο στο οποίο δύο από τις πλευρές – οι βάσεις του τραπεζίδου, είναι παράλληλες μεταξύ τους. Αν σχεδιάσετε διαγώνιες σε ένα τραπέζιο, σχηματίζουν μια σειρά από όμοια τρίγωνα, και οι αναλογικές σχέσεις των πλευρών τους οδηγούν στην κύρια ιδιότητα του τραπεζίδου, συνδυάζοντας τις διαγώνιες του τραπεζίδου και τις τέσσερις πλευρές του:
d12+d22=c2+d2+2ab , όπου a και b – αυτά είναι τα βάσεις του τραπεζίδου, και c και d – οι πλευρικές πλευρές του.
Αυτές οι ίδιες ιδιότητες των όμοιων και ισοδύναμων τριγώνων που σχηματίζονται από τις διαγώνιες καθορίζουν τις ακόλουθες ξεχωριστές φόρμουλες για τις διαγώνιες του τραπεζίδου μέσω των πλευρών:
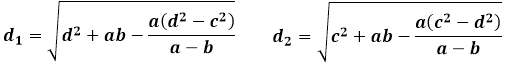
Στους δεδομένους τύπους, το μήκος της διαγωνίου d1 δηλώνει τη διαγώνιο του τραπεζίδου, που σχηματίζει ένα τρίγωνο με τη βάση του τραπεζίδου a και την πλευρική πλευρά d, και το μήκος της διαγωνίου d2 είναι ίσο σε τιμή, αντίστοιχα, με τη γραμμή που συνδέει τη βάση του τραπεζίδου b και την πλευρική πλευρά c.
