Πρόσθεση Κλασμάτων
Πρόσθεση Κλασμάτων με Ίδιους Παρονομαστές:
Ορισμός: Το άθροισμα κλασμάτων με ίδιους παρονομαστές ονομάζεται κλάσμα του οποίου ο αριθμητής είναι ίσος με το άθροισμα των αριθμητών των αρχικών κλασμάτων, με παρονομαστή ίσο με τον παρονομαστή και των δύο κλασμάτων.Τύπος
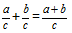
Ας προσθέσουμε δύο κλάσματα με ίδιους παρονομαστές
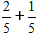
Σύμφωνα με τον τύπο, προσθέτουμε τους αριθμητές, και κρατάμε τον παρονομαστή ίδιο
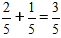
Σημαντικό: Αν είναι δυνατόν, γράφουμε το απλοποιημένο κλάσμα στην τελική απάντηση.
Παράδειγμα:
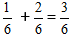Κατά την απλοποίηση του κλάσματος, παίρνουμε τον αριθμό 1/2 Πρόσθεση Κλασμάτων με Διάφορους Παρονομαστές:
Ορισμός: Για να βρείτε το άθροισμα κλασμάτων με διάφορους παρονομαστές, πρώτα φέρτε τα κλάσματα σε κοινό παρονομαστή, και στη συνέχεια προσθέστε τα ως κλάσματα με ίδιους παρονομαστές.Άσκηση:
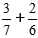
Διαδικασία λύσης:
1) Φέρνουμε τα κλάσματα σε κοινό παρονομαστή.
Για να το κάνουμε αυτό, βρίσκουμε ΕΚΠ - Ελάχιστο Κοινό Πολλαπλάσιο, για παρονομαστές 7 και 6, αυτός ο αριθμός είναι 42.
Διαιρούμε τον αριθμό 42 με τους παρονομαστές των κλασμάτων 3/7 και 2/6
Έτσι, βρήκαμε τους επιπλέον πολλαπλασιαστές.
Στη συνέχεια, πολλαπλασιάζουμε τα κλάσματα με τους επιπλέον πολλαπλασιαστές και παίρνουμε την έκφραση:
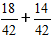
2) Προσθέτουμε τα κλάσματα.
Στην περίπτωσή μας, το κλάσμα μπορεί να απλοποιηθεί κατά 2, και στην τελική απάντηση, γράφουμε τον αριθμό 16/21
Πρόσθεση Κλάσματος και Ακέραιου Αριθμού:
Ορισμός: Για να προσθέσετε ένα κλάσμα σε έναν ακέραιο αριθμό, πρώτα αντιπροσωπεύστε τον ακέραιο αριθμό ως κλάσμα με παρονομαστή ίσο με 1.Αλγόριθμος Υπολογισμού:
1) Φέρνουμε τα κλάσματα σε κοινό παρονομαστή.
2) Προσθέτουμε τα κλάσματα
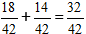
3) Αν είναι δυνατόν, απλοποιήστε το προκύπτον κλάσμα.
4) Αν το αποτέλεσμα είναι ένα ακανονικό κλάσμα, υπολογίστε το ακέραιο μέρος από αυτό.
Παράδειγμα:
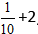
Λύση:
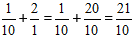
Υπολογίστε το ακέραιο μέρος, και πάρτε την απάντηση
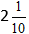
Πρόσθεση Μεικτών Κλασμάτων:
Ορισμός: Για να προσθέσετε μεικτά κλάσματα πρέπει να προσθέσετε ξεχωριστά τα ακέραια μέρη, και ξεχωριστά τα κλασματικά μέρη.Τύπος
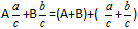
Παράδειγμα:
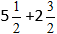
Υποκαθιστούμε τους αριθμούς στον τύπο:
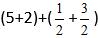
Παίρνουμε:
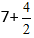
Από το κλάσμα, υπολογίστε το ακέραιο μέρος καθώς είναι ακανονικό, και πάρτε την έκφραση 7+2=9.