Trapetsi Diagonaalid
Trapets on ebatavaline nelinurk, mille kaks külge – trapetsi alused, on omavahel paralleelsed. Kui joonistada trapetsisse diagonaalid, moodustavad need rea sarnaseid kolmnurki ja nende külgede proportsionaalsed suhted viivad trapetsi põhivarani, ühendades trapetsi diagonaalid ja selle neli külge:
d12+d22=c2+d2+2ab , kus a ja b – need on trapetsi alused ja c ja d – tema külgmised küljed.
Need samad omadused sarnaseid ja võrdseid kolmnurke, mida diagonaalid moodustavad, määravad järgmised eraldi valemid trapetsi diagonaalide jaoks läbi külgede:
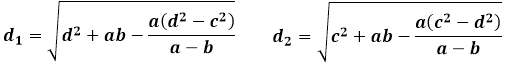
Antud valemites diagonaali pikkus d1 tähistab trapetsi diagonaali, mis moodustab kolmnurga trapetsi alusega a ja külgmise küljega d, ja diagonaali pikkus d2 on väärtuselt võrdne joonega, mis ühendab trapetsi alust b ja külgmist külge c.
