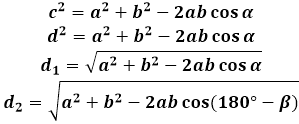Paralleelogrammi Diagonaalid

Rööpkülik on nelinurk, mille vastasküljed on paralleelsed ja võrdsed. Järelikult, vastasrööpküliku nurgad on samuti üksteisega võrdsed ja kuna nelinurga kõigi nurkade summa on 360 kraadi, siis võib järeldada, et kahe järjestikuse nurga summa on 180 kraadi. See omadus mängib olulist rolli rööpküliku diagonaalide leidmisel, arvestades, et need on erineva pikkusega.

Kuna iga rööpküliku diagonaal jagab selle kaheks võrdseks kolmnurgaks, kasutatakse nende omadusi, et tuletada rööpküliku diagonaali valem.

Mis tahes kolmnurgas on nurk ja sellele vastaskülg üksteise suhtes proportsionaalsed. Rööpküliku puhul tähendab see, et pikem diagonaal asub nürinurga vastas ja lühem diagonaal - teravnurga vastas. Arvestades, et diagonaalide moodustatud kolmnurkade küljed on samad - need on rööpküliku küljed, määrab nende külgede vaheline nurk diagonaali pikkuse, mis arvutatakse valemi abil. Teisisõnu, kui rööpküliku teravnurga väärtus sisestatakse diagonaali valemisse, arvutab kalkulaator lühikese diagonaali pikkuse ja kui nürinurga väärtus - pika.

Et vahetada ühe nurga väärtus teiseks, kasutatakse 180 kraadi ja antud nurga vahet, seega saab kalkulaator samaaegselt arvutada mõlemad diagonaalid.

α=180°-β

Rööpküliku diagonaali valemi tuletamiseks kasutatakse kolmnurga koosinuse teoreemi, mille moodustavad diagonaal ja küljed. Mis tahes sellistes kolmnurkades on diagonaal külg, mis asub rööpküliku nurga vastas, ja vastavalt sellele võrdub selle ruut kahe ülejäänud kolmnurga külje ruutude summaga(rööpküliku puhul) miinus kaks korda samade külgede korrutis antud nurga koosinusega. Rööpküliku diagonaali pikkuse leidmiseks arvutab kalkulaator selle avaldise ruutjuure.