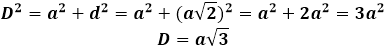Kuubi Diagonaal

Kuup on põhiline geomeetriline keha, kui jutt käib ruumalast ja kolmemõõtmelistest kehadest. Pole juhus, et kolmas aste, mis saadakse kolme samasuguse arvu korrutamisel omavahel (nagu kuubi ruumala leidmisel kuubi ruumala - kolme võrdsest mõõtmest) on nimetatud selle järgi.

Kuubi ainus ja peamine parameeter on selle serv a, kuna kõik kuubi servad on samaväärsed ja esindavad nii pikkust, laiust kui ka kõrgust. Seega määrab ainult üks väärtus kõik võimalikud kuubi mõõtmetega seotud omadused.

Lisaks servadele saab kuubi tippe ühendada diagonaalidega. Diagonaalid võivad läbida kuubi pindasid, sel juhul on need lihtsalt põhja diagonaal või ruudu diagonaal tasapinnas, või võivad diagonaalid olla tõmmatud kuubi sisse, ühendades vastupidiseid aluseid äärmuslikes punktides (tipud).

Et leida kuubi diagonaal läbi selle serva, tuleb esimesena teha lisakonstruktsioon ühe ühendatud põhja diagonaali kujul, siis muutub kuubi diagonaal äsja moodustatud täisnurkse kolmnurga hüpotenuusiks, mille kaatetid on kuubi serv ja põhja diagonaal. Kui ülesande tingimustes on antud kuubi serv, siis tuleb põhja diagonaal esimesena arvutada valemiga: d=a√2

Siis saab kuubi diagonaali väljendada läbi Pythagorase teoreemi, ja see võtab järgmise kuju: