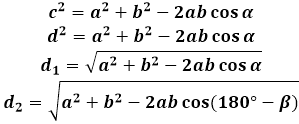平行四辺形の対角線

平行四辺形は、反対側が平行で等しい四辺形です。したがって、反対側の平行四辺形の角度 も互いに等しくなります。四辺形のすべての角度の合計が360度であるため、連続する2つの角度の合計が180度になると結論付けられます。この特性は、平行四辺形の対角線を見つける際に重要な役割を果たします。対角線は異なる長さであることを考慮します。

平行四辺形の各対角線がそれを2つの等しい三角形に分割するので、それらの特性を使用して平行四辺形の対角線の公式を導き出します。

任意の三角形では、角度とそれに対する辺は互いに比例しています。平行四辺形では、長い対角線は鈍角に対して、短い対角線は鋭角に対して配置されます。対角線によって形成される三角形の辺は同じであり、これらは平行四辺形の辺です。これらの辺の間の角度の度数は、公式で計算された対角線の長さを決定します。言い換えれば、平行四辺形の鋭角の値を対角線の公式に代入すると、計算機は短い対角線の長さを計算し、鈍角の値を代入すると、長い対角線を計算します。

一方の角度から他の角度に切り替えるために、180度から与えられた角度の差を使用します。このようにして、計算機は同時に両方の対角線を計算できます。

α=180°-β

平行四辺形の対角線の公式を導き出すために、対角線と辺によって形成される三角形の余弦定理を使用します。これらの三角形のいずれかで、対角線は平行四辺形の角度に対する辺です。そして、その平方は三角形の他の2辺の平方の合計に等しくなります。(平行四辺形の場合)与えられた角度の余弦で同じ辺の積を2倍したものを引きます。平行四辺形の対角線の長さを見つけるために、計算機はこの式の平方根を計算します。