Trapezijos įstrižainės

Trapezija yra nestandartinis keturkampis, kuriame dvi kraštinės – trapecijos pagrindai, yra lygiagrečios viena kitai. Jei nubrėžiate trapecijos įstrižaines, jos suformuoja panašių trikampių seriją, o jų kraštinių proporciniai santykiai lemia pagrindinę trapecijos savybę, sujungiančią trapecijos įstrižaines ir keturias kraštines:
d₁²+d₂²=c²+d²+2ab , kur a ir b – tai yra trapecijos pagrindai, ir c ir d – jos šoninės kraštinės.

Šios pačios panašių ir lygių trikampių, suformuotų įstrižainėmis, savybės nustato šias atskiras trapecijos įstrižainių formules per kraštines:

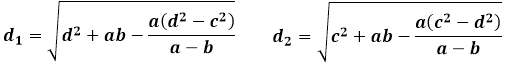
Pateiktose formulėse, įstrižainės ilgis d₁ nurodo trapecijos įstrižainę, kuri suformuoja trikampį su trapecijos pagrindu a ir šonine kraštine d, o įstrižainės ilgis d₂ yra lygus, atitinkamai, linijai, jungiančiai trapecijos pagrindą b ir šoninę kraštinę c.