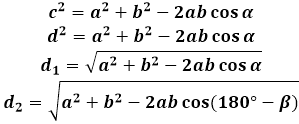Lygiagretainio įstrižainės

Lygiagretainis yra keturkampis, kurio priešingos pusės yra lygiagrečios ir lygios pagal apibrėžimą. Todėl priešingi lygiagretainio kampai taip pat bus lygūs vienas kitam, ir kadangi visų kampų suma keturkampyje yra 360 laipsnių, galima daryti išvadą, kad dviejų iš eilės einančių kampų suma bus 180 laipsnių. Ši savybė atliks svarbų vaidmenį nustatant lygiagretainio įstrižaines, atsižvelgiant į tai, kad jos yra skirtingo ilgio.

Kadangi kiekviena lygiagretainio įstrižainė padalija jį į du lygius trikampius, jų savybės bus naudojamos lygiagretainio įstrižainės formulei išvesti.

Bet kuriame trikampyje, kampas ir prieš jį esanti kraštinė yra proporcingi vienas kitam. Lygiagretainio atveju tai reiškia, kad ilgesnė įstrižainė eis priešais buką kampą, o trumpesnė - priešais aštrų kampą. Atsižvelgiant į tai, kad trikampių, kuriuos sudaro įstrižainės, kraštinės yra tos pačios - tai yra lygiagretainio kraštinės, kampo tarp šių kraštinių laipsnio matas nustato įstrižainės ilgį, apskaičiuojamą pagal formulę. Kitaip tariant, jei įstrižainės formulei įrašomas lygiagretainio aštrus kampas, skaičiuotuvas apskaičiuos trumpos įstrižainės ilgį, o jei bukas kampas - ilgos.

Norėdami pereiti nuo vieno kampo prie kito, naudojamas 180 laipsnių ir duoto kampo skirtumas, todėl skaičiuotuvas vienu metu gali apskaičiuoti abi įstrižaines.

α=180°-β

Norint išvesti lygiagretainio įstrižainės formulę, naudojama kosinuso teorema trikampyje, kurį sudaro įstrižainė su kraštinėmis. Bet kuriame tokiame trikampyje įstrižainė yra kraštinė, priešinga lygiagretainio kampui, ir atitinkamai jos kvadratas lygus dviejų kitų trikampio kraštinių kvadratų sumai (lygiagretainio, šiuo atveju) minus dvigubas tų pačių kraštinių ir duoto kampo kosinuso sandaugos produktas. Norint rasti lygiagretainio įstrižainės ilgį, skaičiuotuvas apskaičiuoja šios išraiškos kvadratinę šaknį.