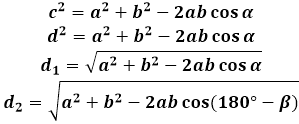Paralelograma Diagonāles

Paralelograms ir četrstūris, kura pretējās malas ir paralēlas un vienādas pēc definīcijas. Attiecīgi, pretējie paralelograma leņķi būs arī vienādi viens ar otru, un tā kā visu leņķu summa četrstūrī ir 360 grādi, var secināt, ka divu secīgu leņķu summa būs 180 grādi. Šī īpašība spēlēs nozīmīgu lomu paralelograma diagonāļu atrašanā, ņemot vērā, ka tās ir dažāda garuma.

Tā kā katra paralelograma diagonāle sadala to divos vienādos trijstūros, to īpašības tiks izmantotas, lai atvasinātu paralelograma diagonāles formulu.

Jebkurā trijstūrī leņķis un tā pretējā mala ir proporcionāli viens otram. Paralelogramam tas nozīmē, ka garākā diagonāle atradīsies pretim platam leņķim, un īsāka diagonāle - pretim asam leņķim. Ņemot vērā, ka trijstūra, ko veido diagonāles, malas ir tās pašas - tās ir paralelograma malas, leņķa starp šīm malām pakāpe nosaka diagonāles garumu, ko aprēķina pēc formulas. Citiem vārdiem sakot, ja paralelograma asā leņķa vērtība tiek ievietota diagonāles formulā, kalkulators aprēķinās īsās diagonāles garumu, un ja platā leņķa vērtība - garo.

Lai pārietu no viena leņķa uz otru, tiek izmantota 180 grādu un dotā leņķa starpība, tādējādi kalkulators var vienlaicīgi aprēķināt abas diagonāles.

α=180°-β

Lai izvadītu paralelograma diagonāles formulu, tiek izmantota kosinusa teorēma trijstūrī, ko veido diagonāle ar malām. Jebkurā no šādiem trijstūriem diagonāle ir mala, kas atrodas pretim paralelograma leņķim, un attiecīgi tās kvadrāts ir vienāds ar kvadrātu summu abām citām trijstūra malām (paralelograma, šajā gadījumā) mīnus divreiz produkts no tām pašām malām ar dotā leņķa kosinusu. Lai atrastu paralelograma diagonāles garumu, kalkulators aprēķina šīs izteiksmes kvadrātsakni.