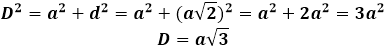Kubikveida Diagonāle

Kubs ir pamata ģeometrisks ķermenis, kad runa ir par tilpumu un tilpuma ķermeņiem. Nav pārsteidzoši, ka trešā pakāpe, kas tiek iegūta, reizinot trīs vienādus skaitļus kopā (kā, aprēķinot kuba tilpumu - trīs tā vienādi mērījumi) ir nosaukta tā godā.

Galvenais un vienīgais kuba parametrs ir tā mala a, jo visas kuba malas ir vienādas un pārstāv gan garumu, platumu, gan augstumu. Attiecīgi tikai viena vērtība nosaka visas iespējamas kuba īpašības, kas saistītas ar tā izmēriem.

Papildus malām kuba virsotnes var savienot ar diagonālēm. Diagonāles var šķērsot kuba sejas, tādā gadījumā tās būs vienkārši pamatnes diagonāle vai kvadrāta diagonāle plaknē, vai arī diagonāles var tikt vilktas pašā kubā, savienojot pretējās pamatnes galējās punktos (virsotnēs).

Lai atrastu kuba diagonāli caur tā malu, vispirms ir jāveic papildu konstrukcija viena no savienotajām pamatnēm veidā, tad kuba diagonāle kļūst par jaunizveidotā taisnā trijstūra hipotenūzu, kuras kājas ir kuba mala un pamatnes diagonāle. Ja kuba mala ir dota uzdevuma nosacījumos, tad vispirms jāaprēķina pamatnes kvadrāta diagonāle, izmantojot formulu: d=a√2

Tad kuba diagonāle var tikt izteikta caur Pitagora teorēmu, un tā iegūs šādu formu: