Trapezium Diagonalen

Een trapezium is een onconventionele vierhoek waarin twee van de zijden – de basis van het trapezium, parallel aan elkaar zijn. Als je diagonalen in een trapezium tekent, vormen ze een reeks van vergelijkbare driehoeken, en de proportionele relaties van hun zijden leiden tot de belangrijkste eigenschap van het trapezium, die de diagonalen van het trapezium en zijn vier zijden combineert:
d₁²+d₂²=c²+d²+2ab , waar a en b – dit zijn de basis van het trapezium, en c en d – zijn laterale zijden.

Dezezelfde eigenschappen van de vergelijkbare en gelijke driehoeken gevormd door de diagonalen bepalen de volgende afzonderlijke formules voor de trapezium diagonalen door de zijden:

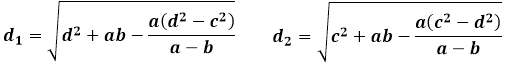
In de gegeven formules, de lengte van de diagonaal d₁ duidt de diagonaal van het trapezium aan, die een driehoek vormt met de basis van het trapezium a en de laterale zijde d, en de lengte van de diagonaal d₂ is in waarde gelijk aan de lijn die de basis van het trapezium verbindt b en de laterale zijde c.