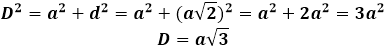Kubus Diagonaal

Een kubus is een basis geometrisch lichaam als het gaat om volume en volumetrische lichamen. Niet verrassend is de derde macht, die wordt verkregen door driemaal dezelfde getallen met elkaar te vermenigvuldigen (zoals bij het vinden van het volume van een kubus - drie van zijn identieke metingen) is naar hem vernoemd.

De belangrijkste en enige parameter van de kubus is zijn rib a, aangezien alle ribben van een kubus congruent zijn en zowel lengte, breedte als hoogte vertegenwoordigen. Dienovereenkomstig bepaalt slechts één waarde alle mogelijke kenmerken van de kubus die verband houden met zijn afmetingen.

Naast de ribben kunnen de hoekpunten van de kubus worden verbonden door diagonalen. Diagonalen kunnen door de kubusvlakken lopen, in welk geval ze gewoon de basisdiagonaal of de vierkantdiagonaal in het vlak zullen zijn, of de diagonalen kunnen in de kubus zelf worden getekend, de tegenovergestelde basis op extreme punten verbindend (hoekpunten).

Om de diagonaal van de kubus te vinden via zijn rib, moet je eerst een extra constructie maken in de vorm van de diagonaal van een van de verbonden basis, dan wordt de diagonaal van de kubus de hypotenusa van de nieuw gevormde rechthoekige driehoek, waarvan de benen de rib van de kubus en de basisdiagonaal zijn. Als de rib van de kubus wordt gegeven door de voorwaarden van het probleem, moet de diagonaal van het vierkant aan de basis eerst worden berekend met behulp van de formule: d=a√2

Dan kan de diagonaal van de kubus worden uitgedrukt via de stelling van Pythagoras, en het zal de volgende vorm aannemen: