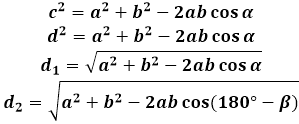Parallellogram Diagonalen

Een parallellogram is een vierhoek waarvan de tegenoverliggende zijden parallel en gelijk zijn volgens de definitie. Bijgevolg zullen de tegenoverliggende hoeken van het parallellogram ook gelijk aan elkaar zijn, en aangezien de som van alle hoeken in een vierhoek 360 graden is, kan worden geconcludeerd dat de som van twee opeenvolgende hoeken 180 graden zal zijn. Deze eigenschap zal een belangrijke rol spelen bij het vinden van de diagonalen van het parallellogram, aangezien ze van verschillende lengte zijn.

Aangezien elke diagonaal van een parallellogram het in twee gelijke driehoeken verdeelt, zullen hun eigenschappen worden gebruikt om de formule voor de diagonaal van een parallellogram af te leiden.

In elke driehoek zijn de hoek en de zijde ertegenover evenredig aan elkaar. Voor een parallellogram betekent dit dat de langere diagonaal tegenover de stompe hoek zal liggen, en de kortere diagonaal - tegenover de scherpe hoek. Aangezien de zijden van de driehoeken gevormd door de diagonalen hetzelfde zijn - dit zijn de zijden van het parallellogram, bepaalt de hoekmaat tussen deze zijden de lengte van de diagonaal, berekend met de formule. Met andere woorden, als de waarde van de scherpe hoek van het parallellogram in de formule voor de diagonaal wordt ingevoerd, zal de rekenmachine de lengte van de korte diagonaal berekenen, en als de waarde van de stompe hoek wordt ingevoerd - de lange.

Om van de ene hoek naar de andere over te schakelen, wordt het verschil van 180 graden en de gegeven hoek gebruikt, zodat de rekenmachine tegelijkertijd beide diagonalen kan berekenen.

α=180°-β

Om de formule voor de diagonaal van een parallellogram af te leiden, wordt de cosinusregel in de driehoek gevormd door de diagonaal met de zijden gebruikt. In een van dergelijke driehoeken is de diagonaal de zijde tegenover de hoek van het parallellogram, en overeenkomstig is zijn kwadraat gelijk aan de som van de kwadraten van de twee andere zijden van de driehoek (van het parallellogram, in dit geval) min tweemaal het product van dezelfde zijden door de cosinus van de gegeven hoek. Om de lengte van de diagonaal van het parallellogram te vinden, berekent de rekenmachine de vierkantswortel van deze uitdrukking.