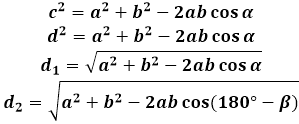Parallellogramdiagonaler
Et parallellogram er en firkant der de motsatte sidene er parallelle og like per definisjon. Følgelig, de motsatte vinklene i parallellogrammet vil også være like hverandre, og siden summen av alle vinkler i en firkant er 360 grader, kan det konkluderes med at summen av to påfølgende vinkler vil være 180 grader. Denne egenskapen vil spille en betydelig rolle i å finne diagonalene i parallellogrammet, med tanke på at de er av forskjellig lengde.
Siden hver diagonal i et parallellogram deler det i to like trekanter, vil deres egenskaper bli brukt til å utlede formelen for diagonalen i et parallellogram.
I en hvilken som helst trekant er vinkelen og siden som er motstående til den proporsjonal med hverandre. For et parallellogram betyr dette at den lengre diagonalen vil ligge mot den sløve vinkelen, og den kortere diagonalen - mot den spisse vinkelen. Med tanke på at sidene av trekantene dannet av diagonalene er de samme - dette er sidene av parallellogrammet, bestemmer grademålet på vinkelen mellom disse sidene lengden på diagonalen, beregnet ved formelen. Med andre ord, hvis verdien av den spisse vinkelen til parallellogrammet settes inn i formelen for diagonalen, vil kalkulatoren beregne lengden på den korte diagonalen, og hvis verdien av den sløve vinkelen settes inn - den lange.
For å bytte fra en vinkel til en annen brukes forskjellen på 180 grader og den gitte vinkelen, slik at kalkulatoren kan samtidig beregne begge diagonalene.
α=180°-β
For å utlede formelen for diagonalen i et parallellogram, brukes cosinussetningen i trekanten dannet av diagonalen med sidene. I en hvilken som helst av slike trekanter er diagonalen siden som er motstående til parallellogrammets vinkel, og følgelig er kvadratet lik summen av kvadratene til de to andre sidene av trekanten (av parallellogrammet, i dette tilfellet) minus to ganger produktet av de samme sidene ved cosinus til den gitte vinkelen. For å finne lengden av diagonalen i parallellogrammet, beregner kalkulatoren kvadratroten av dette uttrykket.