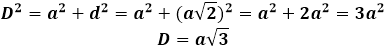Kubediagonal

En kube er en grunnleggende geometrisk kropp når det gjelder volum og volumetriske kropper. Ikke overraskende er den tredje potens, som oppnås ved å multiplisere tre identiske tall sammen (som når man finner volumet av en kube - tre av dens identiske målinger) er oppkalt etter den.

Den viktigste og eneste parameteren til kuben er dens kant a, siden alle kantene av en kube er kongruente og representerer både lengde, bredde og høyde. Følgelig bestemmer kun én verdi alle mulige egenskaper ved kuben relatert til dens dimensjoner.

I tillegg til kantene, kan kubens hjørner kobles sammen med diagonaler. Diagonaler kan passere gjennom kubeansiktene, i så fall vil de ganske enkelt være basediagonalen eller kvadratdiagonalen i planet, eller diagonalene kan trekkes inne i selve kuben, som forbinder motsatte baser ved ekstreme punkter (hjørner).

For å finne kubediagonalen gjennom dens kant, må du først lage en ekstra konstruksjon i form av diagonalen til en av de tilkoblede basene, da blir kubediagonalen hypotenusen til den nylig dannede rettvinklede trekanten, hvis ben er kubens kant og basediagonalen. Hvis kubens kant er gitt av problembetingelsene, må kvadratdiagonalen ved basen først beregnes ved hjelp av formelen: d=a√2

Da kan kubediagonalen uttrykkes gjennom Pythagoras' teorem, og den vil ta følgende form: